题目内容
(本小题满分12分)已知定义在正实数集上的函数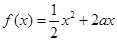 ,
,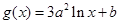 ,其中
,其中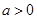 .设两曲线
.设两曲线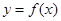 ,
,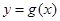 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(1)用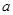 表示
表示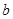 ,并求
,并求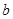 的最大值;
的最大值;
(2)求证: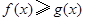 (
(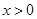 ).
).
【答案】
(1)设 与
与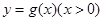 在公共点
在公共点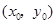 处的切线相同.
处的切线相同.
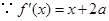 ,
, ,由题意
,由题意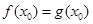 ,
,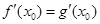 .
.
即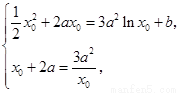 由
由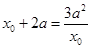
得: ,或
,或 (舍去).
(舍去).
即有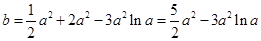 .
.
令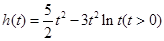 ,则
,则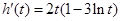 .于是
.于是
当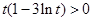 ,即
,即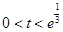 时,
时,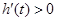 ;
;
当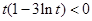 ,即
,即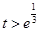 时,
时,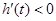 .
.
故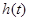 在
在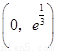 为增函数,在
为增函数,在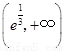 为减函数,
为减函数,
于是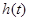 在
在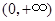 的最大值为
的最大值为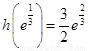 .(2)
.(2)
设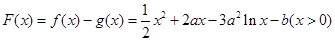 ,
,
则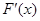
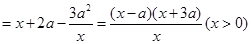 .
.
故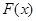 在
在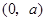 为减函数,在
为减函数,在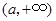 为增函数,
为增函数,
于是函数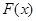 在
在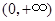 上的最小值是
上的最小值是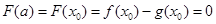 .
.
故当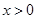 时,有
时,有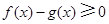 ,即当
,即当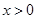 时,
时,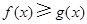
19.经检验,以上所得椭圆的四个顶点无法取到,
故交点轨迹E的方程为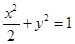
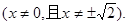
(2)设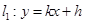
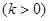 ,则由
,则由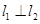 知,
知,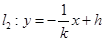 .
.
将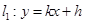 代入
代入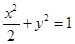 得
得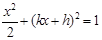 ,
,
即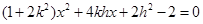 ,
,
若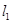 与椭圆相切,则
与椭圆相切,则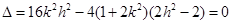 ,即
,即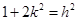 ;
;
同理若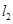 与椭圆相切,则
与椭圆相切,则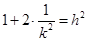 .
.
由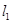 与
与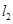 与轨迹E都只有一个交点包含以下四种情况:
与轨迹E都只有一个交点包含以下四种情况:
[1]直线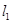 与
与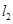 都与椭圆相切,即
都与椭圆相切,即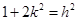 ,且
,且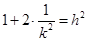 ,消去
,消去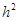 得
得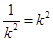 ,即
,即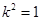 ,
,
从而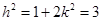 ,即
,即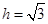 ;
;
[2]直线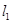 过点
过点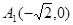 ,而
,而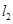 与椭圆相切,此时
与椭圆相切,此时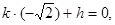
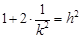 ,解得
,解得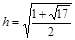 ;
;
[3]直线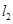 过点
过点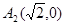 ,而
,而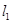 与椭圆相切,此时
与椭圆相切,此时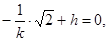
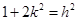 ,解得
,解得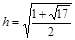 ;
;
[4] 直线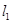 过点
过点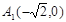 ,而直线
,而直线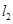 过点
过点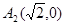 ,此时
,此时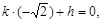
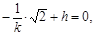
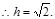
综上所述,h的值为
【解析】略

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目