题目内容
已知数列{an}是首项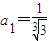 ,公比
,公比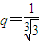 的等比数列,设bn+15log3an=t,常数t∈N*,数列{cn}满足cn=anbn.
的等比数列,设bn+15log3an=t,常数t∈N*,数列{cn}满足cn=anbn.(1)求证:{bn}是等差数列;
(2)若{cn}是递减数列,求t的最小值;
(3)是否存在正整数k,使ck,ck+1,ck+2重新排列后成等比数列?若存在,求k,t的值;若不存在,说明理由.
【答案】分析:(1)由题意知, ,再由
,再由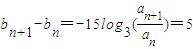 ,得b1=-15log3a1+t=t+5,由此能够证明{bn}是等差数列.
,得b1=-15log3a1+t=t+5,由此能够证明{bn}是等差数列.
(2)由bn=5n+t,知 ,
, 恒成立,再由
恒成立,再由 是递减函数,知当n=1时取最大值,
是递减函数,知当n=1时取最大值, ,由此能求出t的最小值.
,由此能求出t的最小值.
(3)记5k+t=x, ,
, ,
,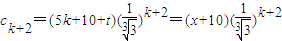 ,再分情况讨论进行求解.
,再分情况讨论进行求解.
解答:解:(1)由题意知, ,(1分)
,(1分)
因为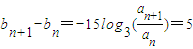 ,b1=-15log3a1+t=t+5
,b1=-15log3a1+t=t+5
∴数列bn是首项为b1=t+5,公差d=5的等差数列.(4分)
(2)由(1)知,bn=5n+t, ,
, 恒成立,即
恒成立,即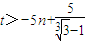 恒成立,(7分)
恒成立,(7分)
因为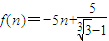 是递减函数,
是递减函数,
所以,当n=1时取最大值, ,(9分)
,(9分)
因而t>6.3,因为t∈N,所以t=7.(10分)
(3)记5k+t=x,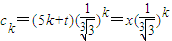 ,
, ,
, .
.
①若ck是等比中项,则由ck+1•ck+2=ck2得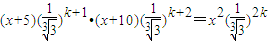 化简得2x2-15x-50=0,解得x=10或
化简得2x2-15x-50=0,解得x=10或 (舍),(11分)
(舍),(11分)
所以5n+t=10,因而 及
及 .
.
又由常数t∈N*,则 舍去,
舍去,
②若ck+1是等比中项,则由ck•ck+2=ck+12得
化简得x(x+10)=(x+5)2,显然不成立.(16分)
③若ck+2是等比中项,则由ck•ck+1=ck+22得
化简得2x2-5x-100=0,因为△=52+4×2×100=25×33不是完全不方数,因而x的值是无理数,显然不成立.
则符合条件的k、t的值为 .(18分)
.(18分)
点评:本题考查等差数列的证明方法、以递减数列为载体求参数的最小值和利用分类讨论思想在等比数列中的运用,解题时要认真审题,注意挖掘题设中的隐含条件.
 ,再由
,再由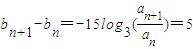 ,得b1=-15log3a1+t=t+5,由此能够证明{bn}是等差数列.
,得b1=-15log3a1+t=t+5,由此能够证明{bn}是等差数列.(2)由bn=5n+t,知
 ,
, 恒成立,再由
恒成立,再由 是递减函数,知当n=1时取最大值,
是递减函数,知当n=1时取最大值, ,由此能求出t的最小值.
,由此能求出t的最小值.(3)记5k+t=x,
 ,
, ,
,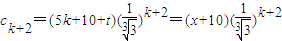 ,再分情况讨论进行求解.
,再分情况讨论进行求解.解答:解:(1)由题意知,
 ,(1分)
,(1分)因为
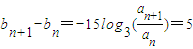 ,b1=-15log3a1+t=t+5
,b1=-15log3a1+t=t+5∴数列bn是首项为b1=t+5,公差d=5的等差数列.(4分)
(2)由(1)知,bn=5n+t,
 ,
, 恒成立,即
恒成立,即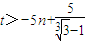 恒成立,(7分)
恒成立,(7分)因为
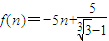 是递减函数,
是递减函数,所以,当n=1时取最大值,
 ,(9分)
,(9分)因而t>6.3,因为t∈N,所以t=7.(10分)
(3)记5k+t=x,
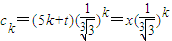 ,
, ,
, .
.①若ck是等比中项,则由ck+1•ck+2=ck2得
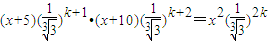 化简得2x2-15x-50=0,解得x=10或
化简得2x2-15x-50=0,解得x=10或 (舍),(11分)
(舍),(11分)所以5n+t=10,因而
 及
及 .
.又由常数t∈N*,则
 舍去,
舍去,②若ck+1是等比中项,则由ck•ck+2=ck+12得

化简得x(x+10)=(x+5)2,显然不成立.(16分)
③若ck+2是等比中项,则由ck•ck+1=ck+22得

化简得2x2-5x-100=0,因为△=52+4×2×100=25×33不是完全不方数,因而x的值是无理数,显然不成立.
则符合条件的k、t的值为
 .(18分)
.(18分)点评:本题考查等差数列的证明方法、以递减数列为载体求参数的最小值和利用分类讨论思想在等比数列中的运用,解题时要认真审题,注意挖掘题设中的隐含条件.

练习册系列答案
相关题目