题目内容
【题目】设![]() 点为圆
点为圆![]() 上的动点,点
上的动点,点![]() 在
在![]() 轴上的投影为
轴上的投影为![]() ,动点
,动点![]() 满足
满足![]() ,动点
,动点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设![]() 的左顶点为
的左顶点为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,
,![]() (
(![]() ,
,![]() 不是左右顶点),且满足
不是左右顶点),且满足![]() ,求证:直线
,求证:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(Ⅰ)设P(x,y),M(x0,y0),由已知条件建立二者之间的关系,利用坐标转移法可得轨迹方程;
(2)由向量条件结合矩形对角线相等可得DA,DB垂直,斜率之积为﹣1,再联立直线与椭圆方程,得根与系数关系,逐步求解得证.
(Ⅰ)设点![]() ,
,![]() ,由题意可知
,由题意可知![]()
∵![]() ,∴
,∴![]() ,
,
即![]() ,
,![]()
又点![]() 在圆
在圆![]() 上 ∴
上 ∴![]()
代入得![]()
即轨迹![]() 的方程为
的方程为![]()
(Ⅱ)由(Ⅰ)可知![]() ,设
,设![]() ,
,![]()
联立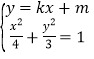 得
得![]()
![]()
![]()
即![]() ,
,![]()
∴![]()
![]()
又![]()
![]()
![]()
∵![]() ∴
∴![]() 即
即![]()
即![]()
![]()
∴![]()
![]()
∴![]()
解得![]() ,
,![]() ,且均满足即
,且均满足即![]()
当![]() 时,
时,![]() 的方程为
的方程为![]() ,直线恒过
,直线恒过![]() ,与已知矛盾;
,与已知矛盾;
当![]() ,
,![]() 的方程为
的方程为![]() ,直线恒过
,直线恒过![]()
所以,直线![]() 过定点,定点坐标为
过定点,定点坐标为![]() .
.

练习册系列答案
相关题目
【题目】高一年级某个班分成7个小组,利用假期参加社会公益服务活动![]() 每个小组必须全员参加
每个小组必须全员参加![]() ,参加活动的次数记录如下:
,参加活动的次数记录如下:
组别 |
|
|
|
|
|
|
|
参加活动次数 | 3 | 2 | 4 | 3 | 3 | 4 | 2 |
![]() Ⅰ
Ⅰ![]() 求该班的7个小组参加社会公益服务活动数的中位数及与平均数v;
求该班的7个小组参加社会公益服务活动数的中位数及与平均数v;
![]() Ⅱ
Ⅱ![]() 从这7个小组中随机选出2个小组在全校进行活动汇报,求“选出的2个小组参加社会公益服务活动次数相等”的概率.
从这7个小组中随机选出2个小组在全校进行活动汇报,求“选出的2个小组参加社会公益服务活动次数相等”的概率.
![]() Ⅲ
Ⅲ![]() 至
至![]() 小组每组有4名同学,
小组每组有4名同学,![]() 小组有5名同学,记“该班学参加社会公益服务活动的平均次数”为
小组有5名同学,记“该班学参加社会公益服务活动的平均次数”为![]() ,写出
,写出![]() 与v的大小关系
与v的大小关系![]() 结论不要求证明
结论不要求证明![]() .
.

