题目内容
已知函数 在区间
在区间 上的最大值与最小值分别为
上的最大值与最小值分别为 ,则
,则 .
.
【答案】
32
【解析】解:∵函数f(x)=x3-12x+8
∴f′(x)=3x2-12
令f′(x)>0,解得x>2或x<-2;令f′(x)<0,解得-2<x<2
故函数在[-2,2]上是减函数,在[-3,-2],[2,3]上是增函数,
所以函数在x=2时取到最小值f(2)=8-24+8=-8,在x=-2时取到最大值f(-2)=-8+24+8=24
即M=24,m=-8∴M-m=32故选C.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在区间
在区间 上的最小值是
上的最小值是 ,则
,则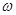 的最小值是___
的最小值是___ 在区间
在区间 上的最大值为2
上的最大值为2 .
. 的值;
的值; 中,角
中,角 ,
, ,
, 所对的边是
所对的边是 ,
, ,
, ,若
,若 ,
, ,
, . 求边长
. 求边长 在区间
在区间 上的最大值与最小值分别为
上的最大值与最小值分别为 ,则
,则 _____________.
_____________.