题目内容
(本题满分12分)已知函数 在区间
在区间 上的最大值为2
上的最大值为2 .
.
(1)求常数 的值;
的值;
(2)在 中,角
中,角 ,
, ,
, 所对的边是
所对的边是 ,
, ,
, ,若
,若 ,
, ,
, 面积为
面积为 . 求边长
. 求边长 .
.
【答案】
(1) (2)
(2)
【解析】
试题分析:(1)由题可知
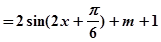 ,
,
∵ ,∴
,∴ ,
,
∵ 函数 在区间
在区间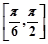 上是增函数,在区间
上是增函数,在区间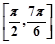 上是减函数,
上是减函数,
∴当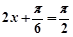 即
即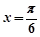 时,函数
时,函数 在区间
在区间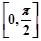 上取到最大值.
上取到最大值.
此时, 得
得 .
……6分
.
……6分
(2)∵ ,∴
,∴ 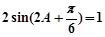 .
.
∴ 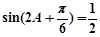 ,解得
,解得 (舍去)或
(舍去)或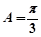 .
.
∵ ,
, ,
,
∴ 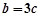 . …………①
. …………①
∵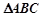 面积为
面积为 ,
,
∴ 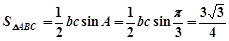 ,
,
即 . …………②
. …………②
由①和②解得 ,
,
∵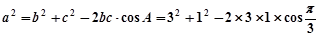
∴  .
……12分
.
……12分
考点:本小题主要考查三角函数式的化简、三角函数的图象和性质、正弦定理和余弦定理的综合应用,考查学生熟练应用公式的能力和运算求解能力.
点评:考查函数的性质,首先要把函数化成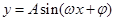 或
或 的形式,这就要求熟练应用二倍角公式、诱导公式和辅助角公式.
的形式,这就要求熟练应用二倍角公式、诱导公式和辅助角公式.

练习册系列答案
相关题目
 的三个内角
的三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 .
. ,且
,且 .(1)求
.(1)求 .求
.求 .
. ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 :
: 的长轴长是短轴长的
的长轴长是短轴长的 倍,
倍, ,
, 是它的左,右焦点.
是它的左,右焦点. ,且
,且 ,
, ,求
,求 作以
作以 (
( 是切点),且使
是切点),且使 ,求动点
,求动点 的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量
的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量 与
与 是共线向量
是共线向量 分别是左右焦点,求
分别是左右焦点,求 的取值范围
的取值范围