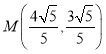题目内容
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 过点
过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)若![]() ,点
,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 与抛物线的另一个交点为
与抛物线的另一个交点为![]() ,直线
,直线![]() 与抛物线的另一个交点为
与抛物线的另一个交点为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)设直线![]() 为
为![]() ,设
,设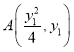 ,
, 为交点,由
为交点,由![]() 得
得![]() ,即得解;(2)求出点
,即得解;(2)求出点![]() 和
和![]() 的坐标分别为
的坐标分别为 ,
, ,利用
,利用![]() 在直线
在直线![]() 上得到
上得到![]() ,设
,设![]() ,利用导数求出函数的取值范围.
,利用导数求出函数的取值范围.
(1)依题意,设直线![]() 为
为![]() ,
,
代入![]() 得
得![]() ,其判别式为
,其判别式为![]() ,
,
∴![]() .
.
设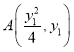 ,
, 为交点,
为交点,
∴![]() ,
,![]() .
.
∵焦点![]() 的坐标为
的坐标为![]() ,
,
∴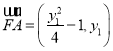 ,
, .
.
∵![]() ,
,
∴
![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() .
.
∵![]() 成立.
成立.
∴![]() .
.
(2)若![]() ,则
,则![]() ,
,
设点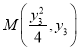 ,
,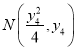 为直线
为直线![]() 、直线
、直线![]() 与抛物线的交点.
与抛物线的交点.
设直线![]() 为
为![]() ,代入
,代入![]() 得
得![]() ,
,
∴![]() ,∴
,∴![]() ,
,
同理可得![]() ,
,
∴点![]() 和
和![]() 的坐标分别为
的坐标分别为 ,
, .
.
又∵![]() 在直线
在直线![]() 上,
上,
∴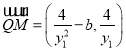 ,
,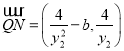 共线,
共线,
∴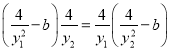 ,
,
∴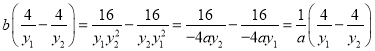 .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() ,设
,设![]() ,
,
∴![]() 在
在![]() 时恒成立,
时恒成立,
∴![]() 在
在![]() 单调递增,
单调递增,![]()
∴![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目