题目内容
【题目】已知圆C:x2+(y﹣1)2=9,直线l:x﹣my+m﹣2=0,且直线l与圆C相交于A、B两点. (Ⅰ)若|AB|=4 ![]() ,求直线l的倾斜角;
,求直线l的倾斜角;
(Ⅱ)若点P(2,1)满足 ![]() =
= ![]() ,求直线l的方程.
,求直线l的方程.
【答案】解:(Ⅰ)若|AB|=4 ![]() ,则圆心到直线的距离为
,则圆心到直线的距离为 ![]() =1, ∴
=1, ∴ ![]() =1,∴m=
=1,∴m= ![]() ,
,
∴直线的斜率为 ![]() ,
,
∴直线l的倾斜角为30°或150°;
(Ⅱ)若点P(2,1)满足 ![]() =
= ![]() ,则P为AB的中点,
,则P为AB的中点,
∵kCP=0,∴直线l的斜率不存在,
∴直线l的方程为x=2.
【解析】(Ⅰ)若|AB|=4 ![]() ,则圆心到直线的距离为
,则圆心到直线的距离为 ![]() =1,利用点到直线的距离公式,建立方程,即可求直线l的倾斜角;(Ⅱ)若点P(2,1)满足
=1,利用点到直线的距离公式,建立方程,即可求直线l的倾斜角;(Ⅱ)若点P(2,1)满足 ![]() =
= ![]() ,则P为AB的中点,求出直线的斜率,即可求直线l的方程.
,则P为AB的中点,求出直线的斜率,即可求直线l的方程.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
【题目】某百货公司1~6月份的销售量x与利润y的统计数据如表:
月份 | 1 | 2 | 3 | 4 | 5 | 6 |
销售量x(万件) | 10 | 11 | 13 | 12 | 8 | 6 |
利润y(万元) | 22 | 25 | 29 | 26 | 16 | 12 |
(参考公式: ![]() =
= 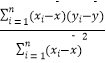 )=
)= 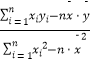 ,
, ![]() .
.
(1)根据2~5月份的统计数据,求出y关于x的回归直线方程 ![]() ;
;
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元,则认为得到的回归直线方程是理想的,试问所得回归直线方程是否理想?