题目内容
平面内动点P（x，y）与A（-2，0），B（2，0）两点连线的斜率之积为 
，则动点P的轨迹方程为
- A.x2+4y2=4
- B.x2-4y2=4
- C.x2+4y2=4（x≠±2）
- D.x2-4y2=4（x≠±2）
D
分析：表达出PA，PB的斜率，利用平面内动点P（x，y）与A（-2，0），B（2，0）两点连线的斜率之积为，即可求得动点P的轨迹方程．
解答：∵平面内动点P（x，y）与A（-2，0），B（2，0）两点连线的斜率之积为，
∴
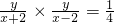（x≠±2）
∴4y2=x2-4
∴x2-4y2=4（x≠±2）
故选D．
点评：本题重点考查轨迹方程，求解的关键是根据平面内动点P（x，y）与A（-2，0），B（2，0）两点连线的斜率之积为，建立等式关系．
分析：表达出PA，PB的斜率，利用平面内动点P（x，y）与A（-2，0），B（2，0）两点连线的斜率之积为
，即可求得动点P的轨迹方程．解答：∵平面内动点P（x，y）与A（-2，0），B（2，0）两点连线的斜率之积为
，∴
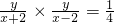（x≠±2）∴4y2=x2-4
∴x2-4y2=4（x≠±2）
故选D．
点评：本题重点考查轨迹方程，求解的关键是根据平面内动点P（x，y）与A（-2，0），B（2，0）两点连线的斜率之积为
，建立等式关系． 
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目