题目内容
已知平面内动点P(x,y)到定点F(1,0)的距离与其到定直线l:x=4的距离之比是| 1 | 2 |
(1)求轨迹M的方程;
(2)证明:当且仅当直线BC垂直于x轴时,△ABC是以BC为底边的等腰三角形;
(3)△ABC的面积是否存在最值?如果存在,求出最值;如果不存在,说明理由.
分析:(1)由题意得
=
,则4[(x-1)2+y2]=(x-4)2,由此能求出轨迹M的方程.
(2)由轨迹M与x轴的负半轴交于点A(-2,0).知直线BC过点A时,A,B,C三点不能构成三角形,故直线BC的斜率不等于0,设直线BC的方程为x=my+1,由
,得(3m2+4)y2+6my-9=0.再由韦达定理进行求解.
(3)设△ABC的面积存在最值.由点A到直线BC的距离d=
,|BC|=
=12
=
.故△ABC的面积S=
|BC|•d=
.由此能够导出△ABC的面积S∈(0,
].
| ||
| |x-4| |
| 1 |
| 2 |
(2)由轨迹M与x轴的负半轴交于点A(-2,0).知直线BC过点A时,A,B,C三点不能构成三角形,故直线BC的斜率不等于0,设直线BC的方程为x=my+1,由
|
(3)设△ABC的面积存在最值.由点A到直线BC的距离d=
| 3 | ||
|
| (x1-x2)2+(y1-y2)2 |
|
| 12(m2+1) |
| 3m2+4 |
| 1 |
| 2 |
18
| ||
| 3m2+4 |
| 9 |
| 2 |
解答:解:(1)由题意得
=
,
则4[(x-1)2+y2]=(x-4)2,
即3x2+4y2=12,∴
+
=1,即是轨迹M的方程.
(2)由(1)易知轨迹M与x轴的负半轴交于点A(-2,0).
直线BC过点A时,A,B,C三点不能构成三角形,故直线BC的斜率不等于0,故可设直线BC的方程为x=my+1,由
,得(3m2+4)y2+6my-9=0.
设B(x1,y1),C(x2,y2),则
y1+y2=-
,y1y2=-
如果△ABC是以BC为底边的等腰三角形,必有|AB|=|AC|,
∴(x1+2)2+y12=(x2+2)2+y22,
∴(x1+x2+4)(x1-x2)+(y1+y2)(y1-y2)=0,
∴[m(y1+y2)+6][m(y1-y2)]+(y1+y2)(y1-y2)=0,
∵y1≠y2,∴(m2+1)(y1+y2)+6m=0,
∴(m2+1)(-
)+6m=0,
∴m=0或
=1(无解),即如果△ABC是以BC为底边的等腰三角形,则m=0,此时直线BC垂直于x轴.
反之,当直线BC垂直于x轴时,直线BC的方程是x=1,
易知B(1,-
),C(1,
)或B(1,
),C(1,-
),
此时|BC|=3,|AB|=|AC|=
,△ABC是以BC为底边的等腰三角形,
故直线BC垂直于x轴时,△ABC是以BC为底边的等腰三角形.
综上可得:当且仅当直线BC垂直于x轴时,△ABC是以BC为底边的等腰三角形.
(3)存在最大值
,不存在最小值.
设△ABC的面积存在最值.由(2)知点A到直线BC的距离d=
;
|BC|=
=
=
=12
=
.
故△ABC的面积S=
|BC|•d=
.
令t=
,则t≥1且m2=t2-1,则
=
=
,
令g(t)=3t+
,则g′(t)=3-
,当t≥1时g′(t)恒大于0,
故函数g(t)=3t+
在[1,+∞)上单调递增,故函数g(t)的值域为[4,+∞),故
∈(0,
],
所以△ABC的面积S∈(0,
],即△ABC的面积存在最大值
,不存在最小值.
| ||
| |x-4| |
| 1 |
| 2 |
则4[(x-1)2+y2]=(x-4)2,
即3x2+4y2=12,∴
| x2 |
| 4 |
| y2 |
| 3 |
(2)由(1)易知轨迹M与x轴的负半轴交于点A(-2,0).
直线BC过点A时,A,B,C三点不能构成三角形,故直线BC的斜率不等于0,故可设直线BC的方程为x=my+1,由
|
设B(x1,y1),C(x2,y2),则
y1+y2=-
| 6m |
| 3m2+4 |
| 9 |
| 3m2+4 |
如果△ABC是以BC为底边的等腰三角形,必有|AB|=|AC|,
∴(x1+2)2+y12=(x2+2)2+y22,
∴(x1+x2+4)(x1-x2)+(y1+y2)(y1-y2)=0,
∴[m(y1+y2)+6][m(y1-y2)]+(y1+y2)(y1-y2)=0,
∵y1≠y2,∴(m2+1)(y1+y2)+6m=0,
∴(m2+1)(-
| 6m |
| 3m2+4 |
∴m=0或
| m2+1 |
| 3m2+4 |
反之,当直线BC垂直于x轴时,直线BC的方程是x=1,
易知B(1,-
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
此时|BC|=3,|AB|=|AC|=
3
| ||
| 2 |
故直线BC垂直于x轴时,△ABC是以BC为底边的等腰三角形.
综上可得:当且仅当直线BC垂直于x轴时,△ABC是以BC为底边的等腰三角形.
(3)存在最大值
| 9 |
| 2 |
设△ABC的面积存在最值.由(2)知点A到直线BC的距离d=
| 3 | ||
|
|BC|=
| (x1-x2)2+(y1-y2)2 |
=
| (m2+1)(y1-y2)2 |
=
(m2+1)[(3m2+4)2+
|
=12
|
| 12(m2+1) |
| 3m2+4 |
故△ABC的面积S=
| 1 |
| 2 |
18
| ||
| 3m2+4 |
令t=
| 1+m2 |
| ||
| 3m2+4 |
| t |
| 3t2+1 |
| 1 | ||
3t+
|
令g(t)=3t+
| 1 |
| t |
| 1 |
| t2 |
故函数g(t)=3t+
| 1 |
| t |
| 1 |
| g(t) |
| 1 |
| 4 |
所以△ABC的面积S∈(0,
| 9 |
| 2 |
| 9 |
| 2 |
点评:本题考查直线和圆锥曲线的位置关系,具有一定的难度,解题时要认真审题,注意培养解题能力,提高解题技巧.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
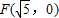 与定直线l:
与定直线l: 的距离之比是常数
的距离之比是常数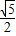 .
. ,设动点P的轨迹为M,轨迹M与x轴的负半轴交于点A,过点F的直线交轨迹M于B、C两点.
,设动点P的轨迹为M,轨迹M与x轴的负半轴交于点A,过点F的直线交轨迹M于B、C两点.