题目内容
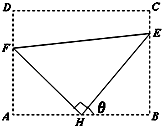
【题目】如图，四棱锥
的底面是正方形，
，
，
，点
分别为棱
的中点.
（1）求证：
∥平面
；
（2）求三棱锥
的体积.
【答案】（1）见解析（2）
【解析】
（1）欲证AF∥平面PCE，根据直线与平面平行的判定定理可知只需证AF与平面PCE内一直线平行，取PC的中点G，连接FG、EG，AF∥EG又EG平面PCE，AF平面PCE，满足定理条件；
（2）三棱锥C﹣BEP的体积可转化成三棱锥P﹣BCE的体积，而PA⊥底面ABCD，从而PA即为三棱锥P﹣BCE的高，根据三棱锥的体积公式进行求解即可．
证明：（1）取PC的中点G，连接FG、EG
∴FG为△CDP的中位线
∴FG
CD
∵四边形ABCD为矩形，E为AB的中点
∴AECD
∴FG
AE
∴四边形AEGF是平行四边形.
∴AF∥EG又EG平面PCE，AF平面PCE
∴AF∥平面PCE.
（2）PA⊥底面ABCD ，在Rt△BCE中，BE=1，BC=2，
∴三棱锥C﹣BEP的体积
VC﹣BEP=VP﹣BCE=
=
.
练习册系列答案
相关题目
