题目内容
设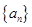 是首项为
是首项为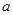 ,公差为
,公差为 的等差数列
的等差数列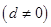 ,
,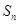 是其前
是其前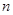 项和.
项和.
(2)记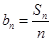 ,
,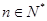 ,且
,且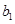 、
、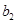 、
、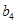 成等比数列,证明:
成等比数列,证明: .
.
【答案】
(1)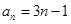 或
或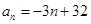 ;(2)详见解析.
;(2)详见解析.
【解析】
试题分析:(1)利用等差数列的性质得到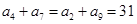 ,结合题中的已知条件将
,结合题中的已知条件将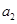 、
、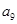 等价转化为一元二次方程
等价转化为一元二次方程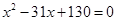 的两根,从而求出
的两根,从而求出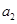 和
和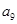 ,最终确定等差数列
,最终确定等差数列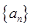 的通项公式;(2)先求出数列
的通项公式;(2)先求出数列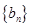 的通项公式(利用
的通项公式(利用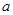 和
和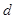 表示),然后通过“
表示),然后通过“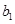 、
、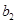 、
、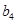 成等比数列”这一条件确定
成等比数列”这一条件确定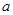 和
和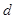 的之间的等量关系,进而将
的之间的等量关系,进而将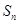 的表达式进一步化简,然后再代数验证
的表达式进一步化简,然后再代数验证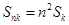 .
.
试题解析:(1)因为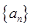 是等差数列,由性质知
是等差数列,由性质知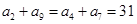 ,
,
所以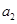 、
、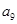 是方程
是方程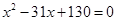 的两个实数根,解得
的两个实数根,解得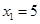 ,
,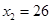 ,
,
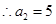 ,
,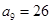 ,
,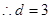 ,
,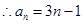 或
或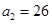 ,
,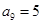 ,
,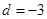 ,
,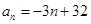 ,
,
即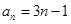 或
或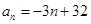 ;
;
(2)证明:由题意知∴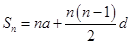 ,∴
,∴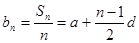 .
.
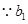 、
、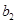 、
、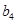 成等比数列,∴
成等比数列,∴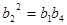 ∴
∴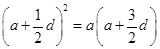 ,
,
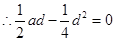
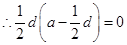 ∵
∵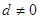 ∴
∴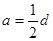 ∴
∴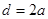 ,
,
∴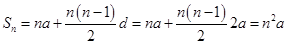 ,
,
∴左边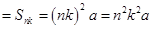 右边
右边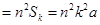 ,
,
∴左边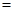 右边∴
右边∴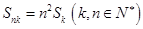 成立.
成立.
考点:1.等差数列的通项公式;2.等差数列求和;3.等比中项的性质

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
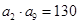
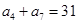 ,求数列
,求数列 是首项为
是首项为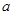 ,公差为
,公差为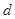 的等差数列
的等差数列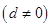 ,
,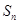 是其前
是其前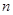 项和.
项和.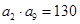
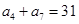 ,求数列
,求数列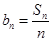 ,
,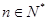 ,且
,且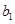 、
、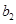 、
、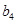 成等比数列,证明:
成等比数列,证明: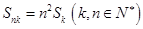 .
.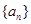 是首项为
是首项为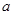 ,公差为
,公差为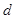 的等差数列(
的等差数列(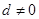 ),
),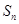 是前
是前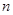 项和. 记
项和. 记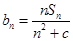 ,
,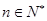 ,其中
,其中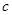 为实数.
为实数.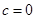 ,且
,且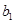 ,
,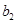 ,
,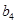 成等比数列,证明:
成等比数列,证明: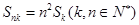 ;
;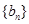 是等差数列,证明
是等差数列,证明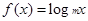 (
(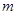 为常数,
为常数,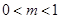 ),且数列
),且数列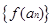 是首项为
是首项为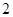 ,公差为
,公差为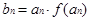 ,当
,当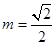 时,求数列
时,求数列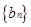 的前
的前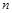 项和
项和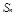 ;
; 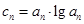 ,如果
,如果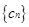 中的每一项恒小于它后面的项,求
中的每一项恒小于它后面的项,求