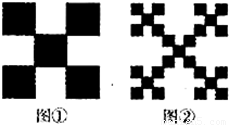题目内容
对一个边长为1的正方形进行如下操作:第一步,将它分割成3×3方格,接着用中心和四个角的5个小正方形,构成如图①所示的几何图形,其面积S1= ;第二步,将图①的5个小正方形中的每个小正方形都进行与第一步相同的操作,得到图②;依此类推,到第n步,所得图形的面积
;第二步,将图①的5个小正方形中的每个小正方形都进行与第一步相同的操作,得到图②;依此类推,到第n步,所得图形的面积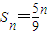 .若将以上操作类比推广到棱长为1的正方体中,则到第n步,所得几何体的体积Vn= .
.若将以上操作类比推广到棱长为1的正方体中,则到第n步,所得几何体的体积Vn= .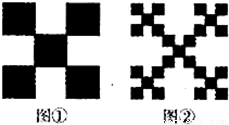
【答案】分析:类比正方形求面积,可得正方体求体积,得出所有体积构成以 为首项,
为首项, 为公比的等比数列,从而可得结论.
为公比的等比数列,从而可得结论.
解答:解:推广到棱长为1的正方体中,第一步,将它分割成3×3×3个正方体,其中心和八个角的9个小正方体,其体积为
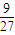 =
= ,第二步,执行同样的操作,其体积为
,第二步,执行同样的操作,其体积为 ,依此类推,到第n步,所有体积构成以
,依此类推,到第n步,所有体积构成以 为首项,
为首项, 为公比的等比数列,
为公比的等比数列,
∴到第n步,所得几何体的体积Vn=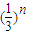
故答案为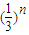 .
.
点评:本题考查数列递推式,考查数列通项的求解,解题的关键是得出所有体积构成以 为首项,
为首项, 为公比的等比数列.
为公比的等比数列.
 为首项,
为首项, 为公比的等比数列,从而可得结论.
为公比的等比数列,从而可得结论.解答:解:推广到棱长为1的正方体中,第一步,将它分割成3×3×3个正方体,其中心和八个角的9个小正方体,其体积为
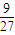 =
= ,第二步,执行同样的操作,其体积为
,第二步,执行同样的操作,其体积为 ,依此类推,到第n步,所有体积构成以
,依此类推,到第n步,所有体积构成以 为首项,
为首项, 为公比的等比数列,
为公比的等比数列,∴到第n步,所得几何体的体积Vn=
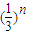
故答案为
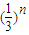 .
.点评:本题考查数列递推式,考查数列通项的求解,解题的关键是得出所有体积构成以
 为首项,
为首项, 为公比的等比数列.
为公比的等比数列. 
练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 (2012•福州模拟)对一个边长为1的正方形进行如下操作:第一步,将它分割成3×3方格,接着用中心和四个角的5个小正方形,构成如图①所示的几何图形,其面积S1=
(2012•福州模拟)对一个边长为1的正方形进行如下操作:第一步,将它分割成3×3方格,接着用中心和四个角的5个小正方形,构成如图①所示的几何图形,其面积S1=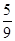 ;第二步,将图①的5个小正方形中的每个小正方形都进行与第一步相同的操作,得到图②;依此类推,到第n步,所得图形的面积
;第二步,将图①的5个小正方形中的每个小正方形都进行与第一步相同的操作,得到图②;依此类推,到第n步,所得图形的面积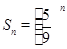 .若将以上操作类比推广到棱长为1的正方体中,则到第n步,所得几何体的体积Vn=____________
.若将以上操作类比推广到棱长为1的正方体中,则到第n步,所得几何体的体积Vn=____________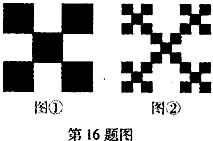
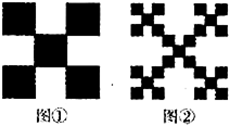 对一个边长为1的正方形进行如下操作:第一步,将它分割成3×3方格,接着用中心和四个角的5个小正方形,构成如图①所示的几何图形,其面积S1=
对一个边长为1的正方形进行如下操作:第一步,将它分割成3×3方格,接着用中心和四个角的5个小正方形,构成如图①所示的几何图形,其面积S1= ;第二步,将图①的5个小正方形中的每个小正方形都进行与第一步相同的操作,得到图②;依此类推,到第n步,所得图形的面积
;第二步,将图①的5个小正方形中的每个小正方形都进行与第一步相同的操作,得到图②;依此类推,到第n步,所得图形的面积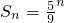 .若将以上操作类比推广到棱长为1的正方体中,则到第n步,所得几何体的体积Vn=________.
.若将以上操作类比推广到棱长为1的正方体中,则到第n步,所得几何体的体积Vn=________. ;第二步,将图①的5个小正方形中的每个小正方形都进行与第一步相同的操作,得到图②;依此类推,到第n步,所得图形的面积
;第二步,将图①的5个小正方形中的每个小正方形都进行与第一步相同的操作,得到图②;依此类推,到第n步,所得图形的面积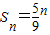 .若将以上操作类比推广到棱长为1的正方体中,则到第n步,所得几何体的体积Vn= .
.若将以上操作类比推广到棱长为1的正方体中,则到第n步,所得几何体的体积Vn= .