��Ŀ����
��֪�� ������N��x��y������ֱ��NP��NQ��б�ʷֱ��Ϊk1��k2����
������N��x��y������ֱ��NP��NQ��б�ʷֱ��Ϊk1��k2���� �����С�?����������������ӡ������ˡ����е�����һ�����㣩������ԭ��ΪO����M��2��1����
�����С�?����������������ӡ������ˡ����е�����һ�����㣩������ԭ��ΪO����M��2��1��������̽��N�Ĺ켣���̣�
��������?����ʾ�˷�������N�Ĺ켣�ټ���P��Q�����Ϊ����C��ֱ��lƽ����ֱ��OM����������C����A��B������ͬ�ĵ㣮
��������ԭ��O����ABΪֱ����Բ���ڲ��������ֱ��l��y���ϵĽؾ�m��ȡֵ��Χ��
�������������AOB��������ֵ����ʱֱ��l�ķ��̣�
���𰸡�������������б�ʹ�ʽֱ��д��k1��k2��Ȼ��ֱ�����üӣ������ˣ������������ö���N�Ĺ켣���̣�
�����������ֱ��l�ķ��̣�����Բ����������Ϊ����x��һԪ���η��̣����ø���ϵ����ϵ�õ�������A��B�ĺ�����ĺ����������ԭ��O����ABΪֱ����Բ���ڲ��õ�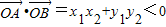 ���������ϵ����ϵ�������m�ķ�Χ��
���������ϵ����ϵ�������m�ķ�Χ��
�����������ҳ���ʽ����ҳ����ɵ㵽ֱ�ߵľ��빫ʽ��������εĸߣ����������ʽ�������䷽������ֵ�����õ�������������ʱ��ֱ�߷��̣�
����⣺������������б�ʵ�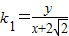 ��
��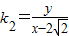
����?����ʾ�ӷ�ʱ��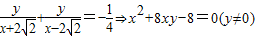 ��
��
����?����ʾ����ʱ��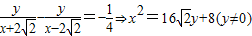 ��
��
����?����ʾ�˷�ʱ��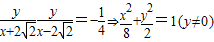 ��
��
����?����ʾ�˷�ʱ��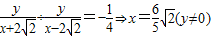 ��
��
��������?����ʾ�˷�������CΪ��Բ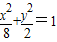 ��
��
��ֱ��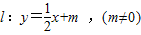 A��x1��y1����B��x2��y2��
A��x1��y1����B��x2��y2��
����ֱ������Բ�ķ��̵ã�x2+2mx+2m2-4=0��
�ɡ���0⇒0��m2��4��
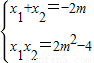 ����*��
����*��
��������Ϊ��O����ABΪֱ����Բ�ڣ���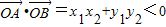 ��
��
��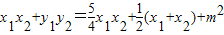 ��
��
����*�������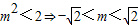
����m��ȡֵ��ΧΪ��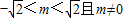
������ԭ��O��ֱ��l�ľ���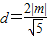 ��
��
�ҳ�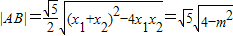
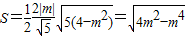 ��
��
��f��m��=4m2-m4=-��m2-2��2+4�ʣ�0��4]
�ʵõ��ҽ���m2=2����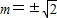 ʱ��
ʱ��
��������ֵSmax=2��
��ʱ��ֱ��l�ķ���Ϊ��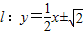 ��
��
���������⿼���˹켣���̵���������ֱ����Բ���ߵĹ�ϵ����������ѧת��˼�뷽������ԭ��O����ABΪֱ����Բ���ڲ�ת��Ϊ������С��0�ǽ�����Ĺؼ���������ѧ���ļ�������������һ���Ѷ���Ŀ��
�����������ֱ��l�ķ��̣�����Բ����������Ϊ����x��һԪ���η��̣����ø���ϵ����ϵ�õ�������A��B�ĺ�����ĺ����������ԭ��O����ABΪֱ����Բ���ڲ��õ�
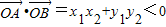 ���������ϵ����ϵ�������m�ķ�Χ��
���������ϵ����ϵ�������m�ķ�Χ�������������ҳ���ʽ����ҳ����ɵ㵽ֱ�ߵľ��빫ʽ��������εĸߣ����������ʽ�������䷽������ֵ�����õ�������������ʱ��ֱ�߷��̣�
����⣺������������б�ʵ�
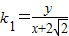 ��
��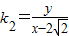
����?����ʾ�ӷ�ʱ��
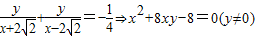 ��
������?����ʾ����ʱ��
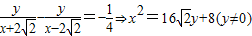 ��
������?����ʾ�˷�ʱ��
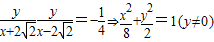 ��
������?����ʾ�˷�ʱ��
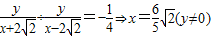 ��
����������?����ʾ�˷�������CΪ��Բ
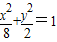 ��
����ֱ��
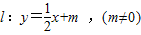 A��x1��y1����B��x2��y2��
A��x1��y1����B��x2��y2������ֱ������Բ�ķ��̵ã�x2+2mx+2m2-4=0��
�ɡ���0⇒0��m2��4��
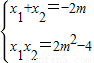 ����*��
����*����������Ϊ��O����ABΪֱ����Բ�ڣ���
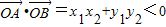 ��
����
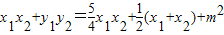 ��
������*�������
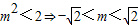
����m��ȡֵ��ΧΪ��
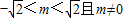
������ԭ��O��ֱ��l�ľ���
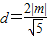 ��
���ҳ�
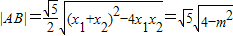
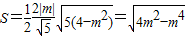 ��
����f��m��=4m2-m4=-��m2-2��2+4�ʣ�0��4]
�ʵõ��ҽ���m2=2����
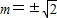 ʱ��
ʱ����������ֵSmax=2��
��ʱ��ֱ��l�ķ���Ϊ��
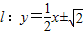 ��
�����������⿼���˹켣���̵���������ֱ����Բ���ߵĹ�ϵ����������ѧת��˼�뷽������ԭ��O����ABΪֱ����Բ���ڲ�ת��Ϊ������С��0�ǽ�����Ĺؼ���������ѧ���ļ�������������һ���Ѷ���Ŀ��

��ϰ��ϵ�д�
�����Ŀ
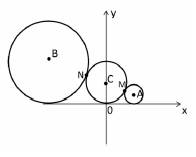
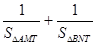 ����СֵΪ2����ֱ��AB�ķ��̣�
����СֵΪ2����ֱ��AB�ķ��̣�