题目内容
已知点F(0，1)，点P在x轴上运动，M点在y轴上，N为动点，且满足
，
．（1）求动点N的轨迹C方程；（2）由直线y= -1上一点Q向曲线C引两条切线，切点分别为A，B，求证：AQ⊥BQ．
已知点F(0，1)，点P在x轴上运动，M点在y轴上，N为动点，且满足
，
．
（1）求动点N的轨迹C方程；
（2）由直线y= -1上一点Q向曲线C引两条切线，切点分别为A，B，求证：AQ⊥BQ．
答案：（1）设N(x，y)．
因，故P的坐标为(
，0)，M(0，-y)，于是，
，
．
因，即得曲线C的方程为x2=4y． ………………………………………………5分
（2）设Q(m，-1)．由题意，两条切线的斜率k均存在，故可设两切线方程为y=k(x-m)-1．
将上述方程代入x2=4y，得x2-4kx+4km+4=0．
依题意，⊿=(-4k)2-4(4km+4)=0，即k2-mk-1=0．
上述方程的两根即为两切线的斜率，
由根与系数的关系，其积为-1，即它们所在直线互相垂直．…………………………………10分
练习册系列答案
小学课时特训系列答案
相关题目
(1)求点P的轨迹方程；
？若存在，求出λ的值，若不存在，请说明理由．
，动点P的轨迹为C，已知圆M过定点D(0，2)，圆心M在轨迹C上运动，且圆M与x轴交于A、B两点，设|DA|＝l1，|DB|＝l2，则
的最大值为
．
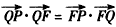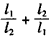的最大值．
，
的最大值。