题目内容
(本题14分)设定义在R上的函数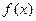 ,对任意
,对任意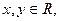 有
有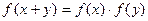 , 且当
, 且当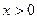 时,恒有
时,恒有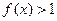 ,若
,若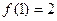 .
.
(1) 求
求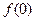 ;
;
(2)求证 :
: 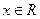 时
时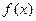 为单调递增函数.
为单调递增函数.
(3)解不等式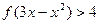 .
.
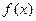 ,对任意
,对任意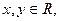 有
有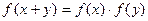 , 且当
, 且当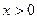 时,恒有
时,恒有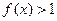 ,若
,若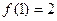 .
.(1)
 求
求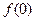 ;
;(2)求证
 :
: 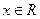 时
时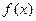 为单调递增函数.
为单调递增函数. (3)解不等式
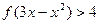 .
.(1)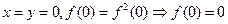 或
或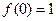
(2)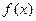 为单调递增函数
为单调递增函数
(3)不等式解集为(1,2).
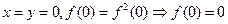 或
或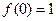
(2)
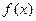 为单调递增函数
为单调递增函数(3)不等式解集为(1,2).
解:(1)令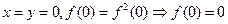 或
或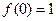 ,
,
又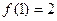 =
=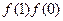 ,故
,故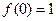 。
。
(2)由于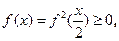 假设存在
假设存在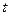 ,使
,使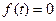 ,则
,则
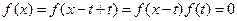 ,与题设矛盾,所以
,与题设矛盾,所以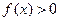 。
。
设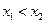 ,
,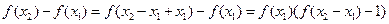 ,由已知
,由已知
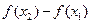
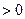 ,于是
,于是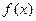 为单调递增函数.
为单调递增函数.
(3)因为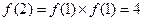 ,不等式
,不等式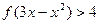 等价于
等价于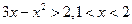 ,不等式解集为(1,2).
,不等式解集为(1,2).
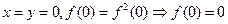 或
或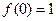 ,
,又
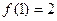 =
=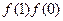 ,故
,故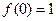 。
。(2)由于
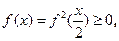 假设存在
假设存在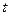 ,使
,使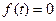 ,则
,则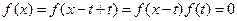 ,与题设矛盾,所以
,与题设矛盾,所以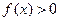 。
。设
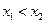 ,
,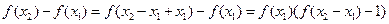 ,由已知
,由已知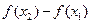
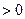 ,于是
,于是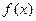 为单调递增函数.
为单调递增函数.(3)因为
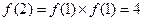 ,不等式
,不等式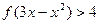 等价于
等价于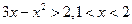 ,不等式解集为(1,2).
,不等式解集为(1,2).
练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 方程
方程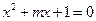 有两
有两 个不等的正实数根,命题
个不等的正实数根,命题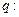 函数
函数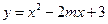 在区间
在区间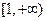 上单调递增. 若命题“
上单调递增. 若命题“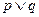 ”是真命题,命题“
”是真命题,命题“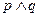 ”是假命题,求实数
”是假命题,求实数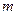 的取值范围.
的取值范围.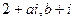 是实系数一元二次方程
是实系数一元二次方程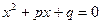 的两根,则
的两根,则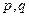 的值为
的值为 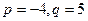
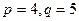
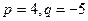
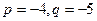
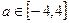 ,
,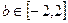 ,并且二次方程
,并且二次方程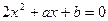 有实根,则方程的根均在区间
有实根,则方程的根均在区间 内的概率为( )
内的概率为( )
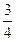

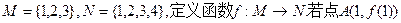 、
、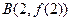 、
、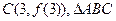 的外接圆圆心为D,且
的外接圆圆心为D,且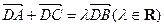 ,则满足条件的函数
,则满足条件的函数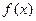 有 ( )
有 ( )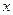 的方程
的方程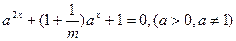 有解,则实数
有解,则实数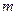 的取值范围是
的取值范围是
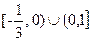
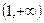
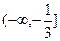
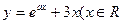 ,
,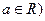 有大于零的极值点,则
有大于零的极值点,则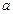 的取值范围是 。
的取值范围是 。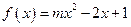 有且仅有一个正实数的零点,则实数
有且仅有一个正实数的零点,则实数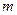 的取值范围是( )
的取值范围是( )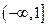
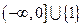
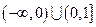
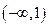
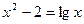 的实数解的个数为 .
的实数解的个数为 .