题目内容
已知抛物线y2=4x的焦点为F,过点P(2,0)的直线交抛物线于A(x1,y1)和B(x2,y2)两点.则:(I)y1 y2= ;(Ⅱ)三角形ABF面积的最小值是 .
【答案】
(I)-8;(Ⅱ)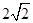 .
.
【解析】
试题分析:(I)①当斜率不存在时,过点P(2,0)的直线为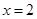 ,此时易知
,此时易知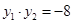 .②当斜率存在时,过点P(2,0)的直线可设为:
.②当斜率存在时,过点P(2,0)的直线可设为: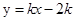 .因为该直线与抛物线
.因为该直线与抛物线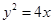 有两个交点,所以
有两个交点,所以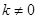 .联立方程
.联立方程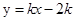 与
与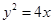 化简得:
化简得: ,由韦达定理得
,由韦达定理得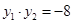 .综合①②知
.综合①②知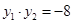 .(Ⅱ)易知焦点
.(Ⅱ)易知焦点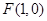 ,①当斜率存在时,
,①当斜率存在时,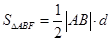 ,其中
,其中 是点
是点 到直线
到直线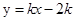 的距离.即
的距离.即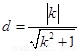 ,
,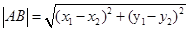 .
.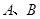 在直线
在直线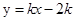 上,
上,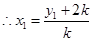 ,
,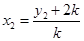 ,
,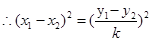 ,
,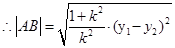 ,
,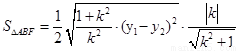
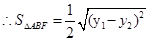
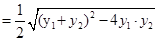 ,其中
,其中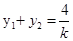 ,
,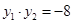 .
.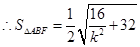
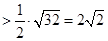 ②当斜率不存在时直线为
②当斜率不存在时直线为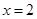 ,此时易知
,此时易知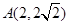 ,
,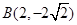 ,
,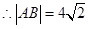 ,点
,点 到直线
到直线 的距离是1,
的距离是1,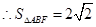 ,综上所述,三角形
,综上所述,三角形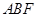 面积的最小值是
面积的最小值是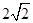 .
.
考点:1.抛物线的简单几何性质;2.直线与圆锥曲线的位置关系;3.点到直线的距离公式.

练习册系列答案
相关题目
 已知抛物线y2=4x,焦点为F,顶点为O,点P(m,n)在抛物线上移动,Q是OP的中点,M是FQ的中点.
已知抛物线y2=4x,焦点为F,顶点为O,点P(m,n)在抛物线上移动,Q是OP的中点,M是FQ的中点.