题目内容
曲线y=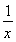 在x=2处的切线斜率为________.
在x=2处的切线斜率为________.
-
【解析】根据导数的几何意义,只要先求出导数以后,将x=2代入即可求解.因为y′=- ,所以y′|x=2=-
,所以y′|x=2=- ,即为切线的斜率.
,即为切线的斜率.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
题目内容
曲线y=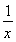 在x=2处的切线斜率为________.
在x=2处的切线斜率为________.
-
【解析】根据导数的几何意义,只要先求出导数以后,将x=2代入即可求解.因为y′=- ,所以y′|x=2=-
,所以y′|x=2=- ,即为切线的斜率.
,即为切线的斜率.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案