题目内容
如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点,F2(1,0)为焦点的抛物线的一部分, 是曲线C1和C2的交点.
是曲线C1和C2的交点.(I)求曲线C1和C2所在的椭圆和抛物线的方程;
(II)过F2作一条与x轴不垂直的直线,与曲线C2交于C,D两点,求△CDF1面积的取值范围.

【答案】分析:(I)先设出抛物线以及椭圆方程,根据F2(1,0)为焦点,求出p=1,得到抛物线方程;再根据( ,
, )在椭圆上,即可求出椭圆方程;
)在椭圆上,即可求出椭圆方程;
(II)设出直线方程x=my+1,并根据条件求出m的取值范围;再联立直线与抛物线方程,根据韦达定理以及|y1-y2|= 求出三角形面积的表达式,最后结合m的取值范围即可求出△CDF1面积的取值范围.
求出三角形面积的表达式,最后结合m的取值范围即可求出△CDF1面积的取值范围.
解答:解:(I)设抛物线方程为:y2=2px,由F2(1,0)为焦点,所以p=1.∴y2=4x
设椭圆方程为 ;代入(
;代入( ,
, ),解得a2=9,
),解得a2=9,
所以椭圆方程为: =1.
=1.
(II)设直线方程为:x=my+1,则m∈(- ,0)∪(0,
,0)∪(0, ).
).
由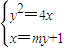 得y2-4my-4=0.
得y2-4my-4=0.
设C(x1,y1),D(x2,y2)
则y1+y2=4m,y1y2=-4.
所以 =
= ×2×|y1-y2|=
×2×|y1-y2|= =4
=4 ,因为m2∈(0,
,因为m2∈(0, ).
).
∴S△∈(4, ).
).
点评:本题主要考查直线与圆锥曲线的位置关系.解决第二问的关键在于把△CDF1面积转化为上下两个三角形面积的和,进而转化为求|y1-y2|的问题.
 ,
, )在椭圆上,即可求出椭圆方程;
)在椭圆上,即可求出椭圆方程;(II)设出直线方程x=my+1,并根据条件求出m的取值范围;再联立直线与抛物线方程,根据韦达定理以及|y1-y2|=
 求出三角形面积的表达式,最后结合m的取值范围即可求出△CDF1面积的取值范围.
求出三角形面积的表达式,最后结合m的取值范围即可求出△CDF1面积的取值范围.解答:解:(I)设抛物线方程为:y2=2px,由F2(1,0)为焦点,所以p=1.∴y2=4x
设椭圆方程为
 ;代入(
;代入( ,
, ),解得a2=9,
),解得a2=9,所以椭圆方程为:
 =1.
=1.(II)设直线方程为:x=my+1,则m∈(-
 ,0)∪(0,
,0)∪(0, ).
).由
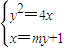 得y2-4my-4=0.
得y2-4my-4=0.设C(x1,y1),D(x2,y2)
则y1+y2=4m,y1y2=-4.
所以
 =
= ×2×|y1-y2|=
×2×|y1-y2|= =4
=4 ,因为m2∈(0,
,因为m2∈(0, ).
).∴S△∈(4,
 ).
).点评:本题主要考查直线与圆锥曲线的位置关系.解决第二问的关键在于把△CDF1面积转化为上下两个三角形面积的和,进而转化为求|y1-y2|的问题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
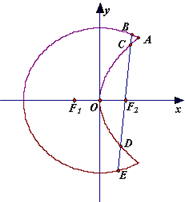 如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|=
如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|=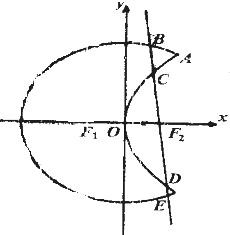 曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点,F2(1,0)为焦点的抛物线的一部分,
曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点,F2(1,0)为焦点的抛物线的一部分,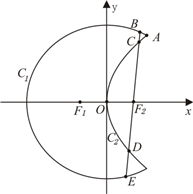 如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点,曲线C1的离心率为
如图,曲线C1是以原点O为中心、F1,F2为焦点的椭圆的一部分,曲线C2是以O为顶点、F2为焦点的抛物线的一部分,A是曲线C1和C2的交点,曲线C1的离心率为 (2012•孝感模拟)如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|=
(2012•孝感模拟)如图,曲线C1是以原点O为中心,F1,F2为焦点的椭圆的一部分.曲线C2是以O为顶点,F2为焦点的抛物线的一部分,A是曲线C1和C2的交点且∠AF2F1为钝角,若|AF1|= 如图,曲线C1是以原点O为中心,F1、F2为焦点的椭圆的一部分,曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分,
如图,曲线C1是以原点O为中心,F1、F2为焦点的椭圆的一部分,曲线C2是以原点O为顶点,F2为焦点的抛物线的一部分,