题目内容
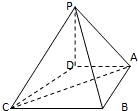 在四棱锥P-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=AD=a,BC=2a,PD⊥底面ABCD.
在四棱锥P-ABCD中,底面ABCD是一直角梯形,∠BAD=90°,AD∥BC,AB=AD=a,BC=2a,PD⊥底面ABCD.
(1)在PD上是否存在一点F,使得PB∥平面ACF,若存在,求出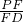 的值;若不存在,试说明理由;
的值;若不存在,试说明理由;
(2)在(1)的条件下,若PA与CD所成的角为60°,求二面角A-CF-D的余弦值.
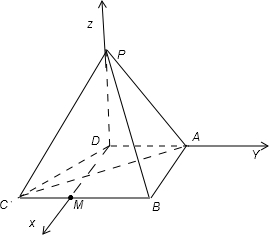 解:(1)建立如图所示的空间直角坐标系:
解:(1)建立如图所示的空间直角坐标系:D(0,0,0),A(0,a,0),B(a,a,0),C(a,-a,0),
设PD=b,则P(0,0,b),假设存在点F使PB∥平面ACF,F(0,0,λb)(0<λ<1)
设平面ACF的一个法向量为
 ,
,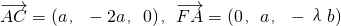 ,
,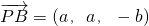
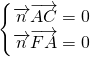 ,
,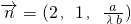 ,
,所以
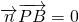 ,
,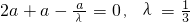 ,所以
,所以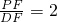 ,
,(2)
 ,
,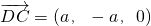 ,
,因为PA与CD所成的角为60°
所以
 =
=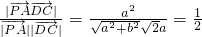 ,
,则a=b,
由(1)知平面ACF的一个法向量为
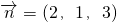
因为∠BAD=90°,AB=AD=a,BC=2a,所以
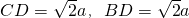 ,
,所以BC2=CD2+BD2,所以BD⊥BC,
又PD⊥底面ABCD,则BD⊥平面CDF,
所以
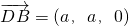 是平面CDF的一个法向量,
是平面CDF的一个法向量,所以
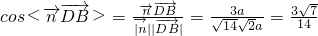 ,
,所以二面角的余弦值为
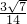 .
.分析:(1)由题意建立空间直角坐标系,假设存在点F使PB∥平面ACF,先写出坐标含有变量,在利用平面法向量的定义建立方程解出即可;
(2)坐标写出后因为PA与CD所成的角为60°,利用夹角建立坐标设出的变量的方程,然后利用两平面的法向量的夹角求出所求的二面角的大小.
点评:此题重点考查了利用条件恰当的建立了空间直角坐标系,先设出坐标用未知的变量表示,在利用平面法向量的知识建立方程进行求解,还利用向量求出二面角的大小.

练习册系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点
如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点 如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2 (2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,
(2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,