题目内容
边长为a的正方形ABCD沿对角线BD折叠成直二面角后,AC的长为
- A.a
- B.
 a
a - C.
 a
a - D.
 a
a
A
分析:取BD的中点E,连接DE,BE,根据正方形可知EA⊥BD,CE⊥BD,则∠AEC为二面角A-BD-C的平面角,在三角形AEC中求出AC的长.
解答: 解:AD=DC=AB=BC=a,
解:AD=DC=AB=BC=a,
取DB的中点E,连接AE,CE,EC=AE= a.
a.
则EA⊥BD,CE⊥BD
,则∠AEC为二面角A-BD-C的平面角
∴∠AEC=90°
∴AC=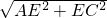 =a.
=a.
故选:A.
点评:本题主要是在折叠问题中考查两点间的距离.折叠问题要注意分清在折叠前后哪些量发生了变化,哪些量没变.
分析:取BD的中点E,连接DE,BE,根据正方形可知EA⊥BD,CE⊥BD,则∠AEC为二面角A-BD-C的平面角,在三角形AEC中求出AC的长.
解答:
 解:AD=DC=AB=BC=a,
解:AD=DC=AB=BC=a,取DB的中点E,连接AE,CE,EC=AE=
 a.
a.则EA⊥BD,CE⊥BD
,则∠AEC为二面角A-BD-C的平面角
∴∠AEC=90°
∴AC=
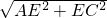 =a.
=a.故选:A.
点评:本题主要是在折叠问题中考查两点间的距离.折叠问题要注意分清在折叠前后哪些量发生了变化,哪些量没变.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a.
如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a. (2012•顺河区一模)选做题:几何证明选讲
(2012•顺河区一模)选做题:几何证明选讲 如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD=
如图,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面PAD⊥底面ABCD,且PA=PD= 已知四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,E为PC上的点且CE:CP=1:4,则在线段AB上是否存在点F使EF∥平面PAD.
已知四棱锥P-ABCD的底面是边长为a的正方形,侧棱PA⊥底面ABCD,E为PC上的点且CE:CP=1:4,则在线段AB上是否存在点F使EF∥平面PAD. (2012•鹰潭一模)在边长为a的正方形ABCD中,E,F分别为BC,CD的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥B-AEF,如图所示.
(2012•鹰潭一模)在边长为a的正方形ABCD中,E,F分别为BC,CD的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,构成一个三棱锥B-AEF,如图所示.