Question

设函数f（x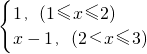）=，g（x）=f（x）-ax，x∈[1，3]，其中a∈（0，1），记函数g（x）的最大值与最小值的差为h（a），则h（a）的最小值是________．

Answer 1

分析：先求出g（x），再分类求出函数的最大值与最小值，可得分段函数，即可求得h（a）的最小值．
解答：由题意，g（x）=f（x）-ax=
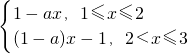
∵1≤x≤2时，g（x）=1-ax，函数单调递减，∴g（x）∈[1-2a，1-a]
2＜x≤3时，g（x）=（1-a）x-1，函数单调递增，∴g（x）∈（1-2a，2-3a]
若1-a＜2-3a，即a＜时，g（x）_max=2-3a；若1-a≥2-3a，即a≥时，g（x）_max=1-a；
∴函数g（x）的最大值与最小值的差为h（a）=
∴
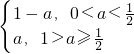
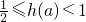
∴h（a）的最小值是
故答案为：
点评：本题考查函数的最值，考查分类讨论的数学思想，考查学生的计算能力，属于中档题．