题目内容
已知α、β均为锐角,且sinα=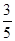 ,tan(α-β)=-
,tan(α-β)=-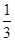 .
.
(1) 求sin(α-β)的值;
(2) 求cosβ的值.
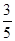 ,tan(α-β)=-
,tan(α-β)=-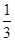 .
.(1) 求sin(α-β)的值;
(2) 求cosβ的值.
(1)-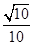 (2)
(2)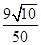
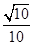 (2)
(2)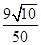
(1) ∵α、β∈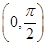 ,∴ -
,∴ -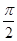 <α-β<
<α-β<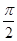 .又tan(α-β)=-
.又tan(α-β)=-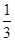 <0,∴ -
<0,∴ -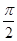 <α-β<0.∴sin(α-β)=-
<α-β<0.∴sin(α-β)=-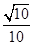 .
.
(2) 由(1)可得,cos(α-β)=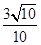 .
.
∵ α为锐角,sinα=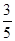 ,∴ cosα=
,∴ cosα=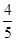 .∴cosβ=cos[α-(α-β)]
.∴cosβ=cos[α-(α-β)]
=cosαcos(α-β)+sinαsin(α-β)=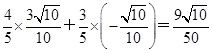 .
.
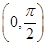 ,∴ -
,∴ -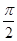 <α-β<
<α-β<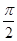 .又tan(α-β)=-
.又tan(α-β)=-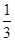 <0,∴ -
<0,∴ -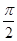 <α-β<0.∴sin(α-β)=-
<α-β<0.∴sin(α-β)=-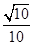 .
.(2) 由(1)可得,cos(α-β)=
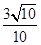 .
.∵ α为锐角,sinα=
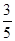 ,∴ cosα=
,∴ cosα=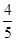 .∴cosβ=cos[α-(α-β)]
.∴cosβ=cos[α-(α-β)]=cosαcos(α-β)+sinαsin(α-β)=
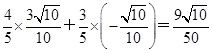 .
.
练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
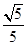 ,sinβ=
,sinβ=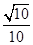 ,且α、β均为锐角,求α+β的值.
,且α、β均为锐角,求α+β的值.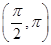 ,则tan2α=________.
,则tan2α=________.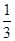 ,
,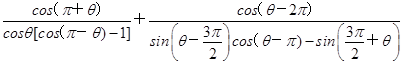 的值.
的值.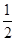 ,且角α在第四象限,计算:
,且角α在第四象限,计算: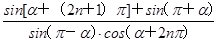 (n∈Z).
(n∈Z).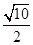 ,则tan 2α=( )
,则tan 2α=( )

 ,则
,则 ( )
( )



 ,则
,则 的值是( )
的值是( )
