题目内容
已知函数f(x)=lnx,其导函数为f′(x),令φ(x)=f′(x).(1)设g(x)=f(x+a)+φ(x+a),求函数g(x)的极值;
(2)设

(i)求证:
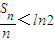 ;
;(ii)是否存在正整数n,使得当n>n时,都有
 成立?若存在,求出一个满足条件的
成立?若存在,求出一个满足条件的n的值;若不存在,请说明理由.
【答案】分析:(1)先求g(x)的导函数,再确定其单调性,从而确定函数的极值;
(2)(i)先证明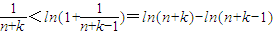 ,再进行累加可证;(ii)又
,再进行累加可证;(ii)又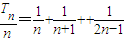 ,
,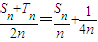 由(i)知
由(i)知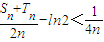 ,从而可以得n>2010时,有
,从而可以得n>2010时,有 ,进一步有
,进一步有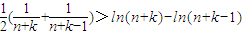 ,从而可证.
,从而可证.
解答:解:(1)因为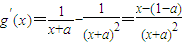 ,∴x∈(-a,1-a]时,函数g(x)为减函数,当x∈[1-a,+∞),函数g(x)为增函数,所以当x=1-a时,函数g(x)取得极小值g(1-a)=1,没有极大值;
,∴x∈(-a,1-a]时,函数g(x)为减函数,当x∈[1-a,+∞),函数g(x)为增函数,所以当x=1-a时,函数g(x)取得极小值g(1-a)=1,没有极大值;
(2)∵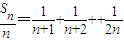
(i)取a=1,由(1)知,当x>0时有g(x)>g(0)=1,即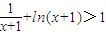 ,∴
,∴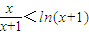 ,即
,即
令 ,即
,即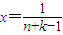 ,∴
,∴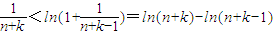
分别取k=1,2,,n并累加得 ,∴
,∴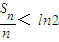
(ii)又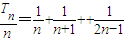 ,∴
,∴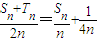
由(i)知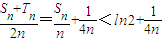 ,即
,即
当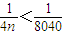 ,即n>2010时,有
,即n>2010时,有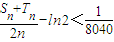
令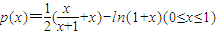 ,∴
,∴
∴p(x)在[0,1)上为增函数,∴p(x)>p(0),∴ ,∴
,∴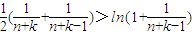
∴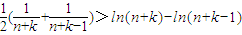
分别取k=1,2,,n并累加得
综上所述,存在正整数n=2010,使得当n>n时,都有 成立.
成立.
点评:本题主要考查了利用导数研究函数的极值,考查不等式的证明,难度较大,有一定的技巧.
(2)(i)先证明
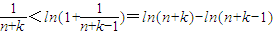 ,再进行累加可证;(ii)又
,再进行累加可证;(ii)又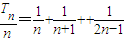 ,
,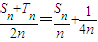 由(i)知
由(i)知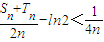 ,从而可以得n>2010时,有
,从而可以得n>2010时,有 ,进一步有
,进一步有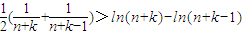 ,从而可证.
,从而可证.解答:解:(1)因为
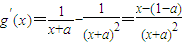 ,∴x∈(-a,1-a]时,函数g(x)为减函数,当x∈[1-a,+∞),函数g(x)为增函数,所以当x=1-a时,函数g(x)取得极小值g(1-a)=1,没有极大值;
,∴x∈(-a,1-a]时,函数g(x)为减函数,当x∈[1-a,+∞),函数g(x)为增函数,所以当x=1-a时,函数g(x)取得极小值g(1-a)=1,没有极大值;(2)∵
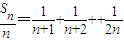
(i)取a=1,由(1)知,当x>0时有g(x)>g(0)=1,即
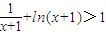 ,∴
,∴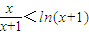 ,即
,即
令
 ,即
,即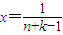 ,∴
,∴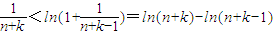
分别取k=1,2,,n并累加得
 ,∴
,∴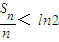
(ii)又
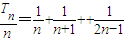 ,∴
,∴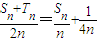
由(i)知
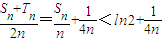 ,即
,即
当
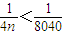 ,即n>2010时,有
,即n>2010时,有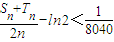
令
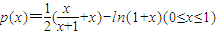 ,∴
,∴
∴p(x)在[0,1)上为增函数,∴p(x)>p(0),∴
 ,∴
,∴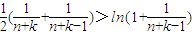
∴
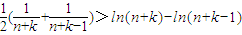
分别取k=1,2,,n并累加得

综上所述,存在正整数n=2010,使得当n>n时,都有
 成立.
成立.点评:本题主要考查了利用导数研究函数的极值,考查不等式的证明,难度较大,有一定的技巧.

练习册系列答案
相关题目