题目内容
两点等分单位圆时,有相应正确关系为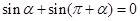 ;三点等分单位圆时,有相应正确关系为
;三点等分单位圆时,有相应正确关系为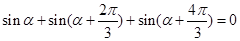 。由此可以推知:四点等分单位圆时的相应正确关系为
。由此可以推知:四点等分单位圆时的相应正确关系为
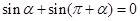 ;三点等分单位圆时,有相应正确关系为
;三点等分单位圆时,有相应正确关系为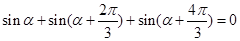 。由此可以推知:四点等分单位圆时的相应正确关系为
。由此可以推知:四点等分单位圆时的相应正确关系为 
试题分析:用两点等分单位圆时,关系为sinα+sin(π+α)=0,两个角的正弦值之和为0,且第一个角为α,第二个角与第一个角的差为:(π+α)-α=π,
用三点等分单位圆时,关系为
 ,此时三个角的正弦值之和为0,且第一个角为α,第二个角与第一个角的差与第三个角与第二个角的差相等,均为有(
,此时三个角的正弦值之和为0,且第一个角为α,第二个角与第一个角的差与第三个角与第二个角的差相等,均为有( )-(
)-( )=(
)=( )-α=
)-α= .
.依此类推,可得当四点等分单位圆时,为四个角正弦值之和为0,且第一个角为α,第二个角为
 +α=
+α= +α,第三个角
+α,第三个角 +α+
+α+ =π+α,第四个角为π+α+
=π+α,第四个角为π+α+ =
= +α,
+α,即其关系为
 。
。点评:中档题,解题的关键在于分析两点等分单位圆与三点等分单位圆的正弦值的个数及角的关系,归纳得出关系式变化的规律。

练习册系列答案
相关题目
 ,
, ,
, ,
, ,
, ,
, ,
, , .则第
, .则第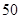 个括号内各数之和为
个括号内各数之和为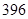



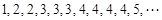 的首项是
的首项是 ,随后两项都是
,随后两项都是 ,接下来
,接下来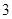 项都是
项都是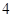 项都是
项都是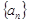 ,若
,若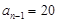 ,
, ,则
,则 .
. ,
, 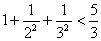 ,
, , ……,根据以上式子可以猜想:
, ……,根据以上式子可以猜想: _______.
_______. 的命题
的命题 满足“若
满足“若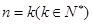 时命题
时命题 时命题
时命题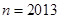 时命题
时命题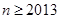 时命题
时命题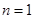 时命题
时命题


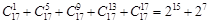
 ,
,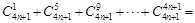 _________.
_________.