题目内容
已知函数f（x）=x3+3bx2+cx+d在（﹣∞，0）上是增函数，在（0，2）上是减函数，且f（x）=0的一个根为﹣b
（Ⅰ）求c的值；
（Ⅱ）求证：f（x）=0还有不同于﹣b的实根x1、x2，且x1、-b、x2成等差数列；
（Ⅲ）若函数f（x）的极大值小于16，求f（1）的取值范围．
（Ⅰ）解：求导函数，可得f'（x）=3x2+6bx+c
∵函数f（x）=x3+3bx2+cx+d在（﹣∞，0）上是增函数，在（0，2）上是减函数，
∴x=0是极大值点，
∴f'（0）=0，∴c=0
（Ⅱ）证明：令f'（x）=0，得x=0或﹣2b
由f（x）的单调性知﹣2b≥2，∴b≤﹣1
∵﹣b是方程f（x）=0的一个根，则（﹣b）3+3b（﹣b）2+d=0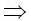
d=﹣2b3
∴f（x）=x3+3bx2﹣2b3=（x+b）（x2+2bx﹣2b2）
方程x2+2bx﹣2b2=0的根的判别式△=4b2﹣4（﹣2b2）=12b2＞0
又（﹣b）2+2b（﹣b）﹣2b2=﹣3b2≠0，
即﹣b不是方程x2+2bx﹣2b2=0的根，
∴f（x）=0有不同于﹣b的根x1、x2．
∴x1+x2=﹣2b，
∴x1、﹣b、x2成等差数列
（Ⅲ）解：根据函数的单调性可知x=0是极大值点
∴f（0）＜16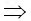
﹣2b3＜16，∴b＞﹣2，
于是﹣2＜b≤﹣1
令g（b）=f（1）=﹣2b3+3b+1
求导g'（b）=﹣6b2+3﹣2＜b≤﹣1时，g'（b）＜0，
∴g（b）在（﹣2，﹣1]上单调递减
∴g（﹣1）≤g（b）＜g（﹣2）即0≤f（1）＜11
∵函数f（x）=x3+3bx2+cx+d在（﹣∞，0）上是增函数，在（0，2）上是减函数，
∴x=0是极大值点，
∴f'（0）=0，∴c=0
（Ⅱ）证明：令f'（x）=0，得x=0或﹣2b
由f（x）的单调性知﹣2b≥2，∴b≤﹣1
∵﹣b是方程f（x）=0的一个根，则（﹣b）3+3b（﹣b）2+d=0
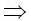d=﹣2b3∴f（x）=x3+3bx2﹣2b3=（x+b）（x2+2bx﹣2b2）
方程x2+2bx﹣2b2=0的根的判别式△=4b2﹣4（﹣2b2）=12b2＞0
又（﹣b）2+2b（﹣b）﹣2b2=﹣3b2≠0，
即﹣b不是方程x2+2bx﹣2b2=0的根，
∴f（x）=0有不同于﹣b的根x1、x2．
∴x1+x2=﹣2b，
∴x1、﹣b、x2成等差数列
（Ⅲ）解：根据函数的单调性可知x=0是极大值点
∴f（0）＜16
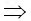﹣2b3＜16，∴b＞﹣2，于是﹣2＜b≤﹣1
令g（b）=f（1）=﹣2b3+3b+1
求导g'（b）=﹣6b2+3﹣2＜b≤﹣1时，g'（b）＜0，
∴g（b）在（﹣2，﹣1]上单调递减
∴g（﹣1）≤g（b）＜g（﹣2）即0≤f（1）＜11
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|