题目内容
【题目】已知椭圆
：
，其焦距为
，若
，则称椭圆为“黄金椭圆”.黄金椭圆有如下性质：“黄金椭圆”的左、右焦点分别是
，
，以
,
，
，
为顶点的菱形
的内切圆过焦点
，
.
（1）类比“黄金椭圆”的定义，试写出“黄金双曲线”的定义；
（2）类比“黄金椭圆”的性质，试写出“黄金双曲线”的性质，并加以证明.
【答案】（1）见解析（2）见解析
【解析】分析：（1）“黄金双曲线“的离心率为
的倒数）．
（2）把椭圆结论中点
与
交换位置得双曲线的性质．
详解：（1）黄金双曲线的定义：已知双曲线
：
，其焦距为
，若
（或写成
），则称双曲线为“黄金双曲线”.
（2）在黄金双曲线的性质：已知黄金双曲线：的左、右焦点分别是
、
，
以、、
、
为顶点的菱形
的内切圆过顶点
、
.
证明：直线
的方程为
，原点到该直线的距离
，
由及
，得
，
将
代入，得
，又将
代入，化简得
，
故直线与圆
相切，同理可证直线
、
均与圆相切，即以、的直径的圆为菱形的内切圆，命题得证.
练习册系列答案
相关题目
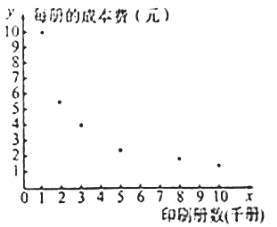
【题目】对某种书籍每册的成本费
（元）与印刷册数
（千册）的数据作了初步处理，得到下面的散点图及一些统计量的值.
|
|
|
|
|
|
|
4.83 | 4.22 | 0.3775 | 60.17 | 0.60 | -39.38 | 4.8 |
其中
，
.
为了预测印刷
千册时每册的成本费，建立了两个回归模型：
，
.
（1）根据散点图，你认为选择哪个模型预测更可靠？（只选出模型即可）
（2）根据所给数据和（1）中的模型选择，求
关于的回归方程，并预测印刷千册时每册的成本费.
附：对于一组数据
，
，…，
，其回归方程
的斜率和截距的最小二乘估计公式分别为：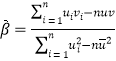
，
.
