题目内容
已知空间任一点O和不共线的三点A,B,C,满足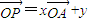
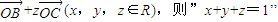 是“点P位于平面ABC内”的( )
是“点P位于平面ABC内”的( )A.充分但不必要条件
B.必要但不充分条件
C.充要条件
D.既不充分也不必要条件
【答案】分析:要寻求四点A、B、C、D共面的充要条件,自然想到共面向量定理.用 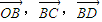 表示出
表示出 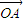 ,进而用
,进而用 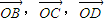 表示
表示 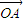 ,三者的系数之和为1即可找出答案.
,三者的系数之和为1即可找出答案.
解答:解:已知空间任一点O和不共线的三点A,B,C,满足
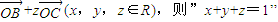 是“点P位于平面ABC内”的充要条件.证明如下:
是“点P位于平面ABC内”的充要条件.证明如下:
(必要性)依题意知,B、C、D三点不共线,
则由共面向量定理的推论知:四点A、B、C、D共面
?对空间任一点O,存在实数x1、y1,使得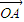 =
= +x1
+x1  +y1
+y1 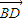
=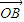 +x1(
+x1( 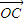 -
-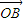 )+y1(
)+y1( 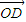 -
-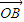 )
)
=(1-x1-y1)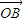 +x1
+x1  +y1
+y1 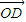 ,
,
取x=1-x1-y1、y=x1、z=y1,
则有 =x
=x 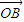 +y
+y 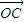 +z
+z 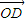 ,且x+y+z=1.
,且x+y+z=1.
(充分性)对于空间任一点O,存在实数x、y、z且x+y+z=1,使得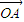 =x
=x 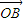 +y
+y 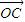 +z
+z 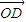 .
.
所以x=1-y-z得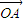 =(1-y-z)
=(1-y-z)  +y
+y  +z
+z  .
.
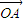 =
=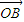 +y
+y 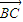 +z
+z  ,即:
,即: ,
,
所以四点A、B、C、D共面.
所以,空间任意无三点共线的四点A、B、C、D共面的充分必要条件是:
对于空间任一点O,存在实数x、y、z且x+y+z=1,使得 =x
=x 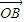 +y
+y 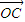 +z
+z  .
.
故选C.
点评:本题考查共线向量与共面向量定理,考查学生分析问题解决问题的能力,是中档题.
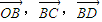 表示出
表示出 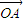 ,进而用
,进而用 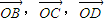 表示
表示 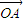 ,三者的系数之和为1即可找出答案.
,三者的系数之和为1即可找出答案.解答:解:已知空间任一点O和不共线的三点A,B,C,满足

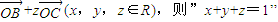 是“点P位于平面ABC内”的充要条件.证明如下:
是“点P位于平面ABC内”的充要条件.证明如下:(必要性)依题意知,B、C、D三点不共线,
则由共面向量定理的推论知:四点A、B、C、D共面
?对空间任一点O,存在实数x1、y1,使得
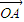 =
= +x1
+x1  +y1
+y1 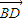
=
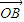 +x1(
+x1( 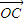 -
-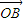 )+y1(
)+y1( 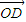 -
-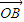 )
)=(1-x1-y1)
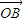 +x1
+x1  +y1
+y1 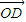 ,
,取x=1-x1-y1、y=x1、z=y1,
则有
 =x
=x 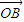 +y
+y 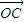 +z
+z 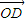 ,且x+y+z=1.
,且x+y+z=1.(充分性)对于空间任一点O,存在实数x、y、z且x+y+z=1,使得
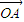 =x
=x 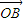 +y
+y 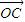 +z
+z 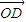 .
.所以x=1-y-z得
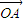 =(1-y-z)
=(1-y-z)  +y
+y  +z
+z  .
.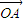 =
=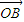 +y
+y 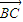 +z
+z  ,即:
,即: ,
,所以四点A、B、C、D共面.
所以,空间任意无三点共线的四点A、B、C、D共面的充分必要条件是:
对于空间任一点O,存在实数x、y、z且x+y+z=1,使得
 =x
=x 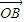 +y
+y 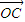 +z
+z  .
.故选C.
点评:本题考查共线向量与共面向量定理,考查学生分析问题解决问题的能力,是中档题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
已知空间任一点O和不共线的三点A,B,C,满足
=x
+y
+z
(x,y,z∈R),则”x+y+z=1”是“点P位于平面ABC内”的( )
| OP |
| OA |
| OB |
| OC |
| A、充分但不必要条件 |
| B、必要但不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
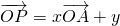
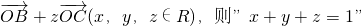 是“点P位于平面ABC内”的
是“点P位于平面ABC内”的