题目内容
已知函数 ,
,
(1)求该函数的最小正周期和最小值;
(2)若 ,求该函数的单调递增区间。
,求该函数的单调递增区间。
(1)
(2)函数的
解析试题分析:(1)先利用两角和差的公式化为单一函数的形式。
(2)运用正弦函数的单调增区间,结合定义域,利用集合的交集运算得到结论。
解:(1) ------3分
------3分
所以  ------6分
------6分
(2) ------8分
------8分
令 ,得到
,得到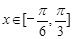 或
或 ,与
,与 取交集, 得到
取交集, 得到 或
或 ,所以,当
,所以,当 时,函数的
时,函数的 . ----12分
. ----12分
考点:本题主要考查了三角函数的图像与性质的综合运用。
点评:解决该试题的关键是利用两角和差的公式将函数化为单一三角函数,然后利用整体思想,结合正弦函数的单调区间得到结论。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,且
,且 .
.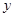 表示成
表示成 的函数
的函数 ,并求
,并求 ,
, 、
、 、
、 分别为
分别为 的三个内角
的三个内角 、
、 、
、 对应的边长,若
对应的边长,若 且
且 ,求
,求 的最大值.
的最大值. ,其中
,其中
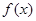 在区间
在区间 上的值域;
上的值域; 中,
中, .
. ,
, 分别是角
分别是角 的对边,
的对边,  ,且
,且
 ,求边
,求边 的一条对称轴为
的一条对称轴为 ,且
,且
 ,且
,且 ,
, ;
; ;
; 的值。
的值。
 的内角,且为钝角,求
的内角,且为钝角,求 的最小值;
的最小值; 是锐角
是锐角 的内角,且
的内角,且 求
求 的图象与
的图象与 轴的交点为
轴的交点为 ,它在
,它在 和
和 .
. 的解析式及
的解析式及 的值;
的值; 满足
满足 ,求
,求 的值。
的值。 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 ,若
,若 ,且
,且 .
. 的值; (2)若
的值; (2)若 ,求△
,求△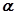 的顶点在原点,始边与
的顶点在原点,始边与 轴的正半轴重合,终边与单位圆相交于点
轴的正半轴重合,终边与单位圆相交于点 .
.  的值;
的值; , 试问该函数
, 试问该函数 的图象可由
的图象可由 的图象经过怎样的平移和伸缩变换得到.
的图象经过怎样的平移和伸缩变换得到.