题目内容
在直二面角α-l-β中,直线a?α,直线b?β,a,b与l斜交,则
- A.a不和b垂直,但可能a∥b
- B.a可能和b垂直,也可能a∥b
- C.a不和b垂直,a也不和b平行
- D.a不和b平行,但可能a⊥b
C
分析:先在l上任取一点P,过P分别在α、β内作a′∥a,b′∥b,在a′上任取一点A,过A作AC⊥l,垂足为C,过C作CB⊥b′交b′于B,连AB,由三垂线定理知AB⊥b′,从而得到∠APB为锐角,说明a不和b垂直,a也不和b平行.
解答: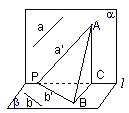 解:如图,在l上任取一点P,过P分别在α、β内作a′∥a,b′∥b,
解:如图,在l上任取一点P,过P分别在α、β内作a′∥a,b′∥b,
在a′上任取一点A,过A作AC⊥l,垂足为C,则AC⊥β,
过C作CB⊥b′交b′于B,连AB,由三垂线定理知AB⊥b′,
∴△APB为直角三角形,故∠APB为锐角.
∴a不和b垂直,a也不和b平行
故选C
点评:本题主要考查了二面角及其度量,以及空间中直线与直线之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于基础题.
分析:先在l上任取一点P,过P分别在α、β内作a′∥a,b′∥b,在a′上任取一点A,过A作AC⊥l,垂足为C,过C作CB⊥b′交b′于B,连AB,由三垂线定理知AB⊥b′,从而得到∠APB为锐角,说明a不和b垂直,a也不和b平行.
解答:
 解:如图,在l上任取一点P,过P分别在α、β内作a′∥a,b′∥b,
解:如图,在l上任取一点P,过P分别在α、β内作a′∥a,b′∥b,在a′上任取一点A,过A作AC⊥l,垂足为C,则AC⊥β,
过C作CB⊥b′交b′于B,连AB,由三垂线定理知AB⊥b′,
∴△APB为直角三角形,故∠APB为锐角.
∴a不和b垂直,a也不和b平行
故选C
点评:本题主要考查了二面角及其度量,以及空间中直线与直线之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
相关题目
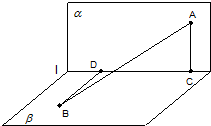 (2006•广州一模)如图,长度为2的线段AB夹在直二面角α-l-β的两个半平面内,A∈α,B∈β,
(2006•广州一模)如图,长度为2的线段AB夹在直二面角α-l-β的两个半平面内,A∈α,B∈β,