题目内容
在直二面角α-β-l中，A∈α，B∈β，AB与α所成角为x，AB与β所成角为y，AB与l所成的角为z，则cos2x+cos2y+sin2z=
2
2
．分析：先分别作出AB与α所成角为x，AB与β所成角为y，AB与l所成角为z，再利用三角函数求解即可．
解答：解：过A、B分别作AC⊥l于C，BD⊥l于D，过B作直线平行于l，过C作直线平行于BD，两直线交于E，连接AD、AC、AE．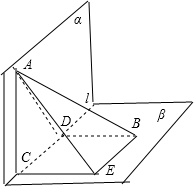
因α一l一β为直二面角，BD在β上，l=α∩β，BD⊥l，故BD⊥α．同理AC⊥β．
又∠BAD、∠ABC分别为AB与α、β所成的角，有∠BAD=x，∠ABC=y．
又EC∥BD，EC⊥l，AC⊥β，有AE⊥l，AE⊥BE，∠EBA=z．
∴cos2x+cos2y+sin2z=
+
+
=2
故答案为：2
因α一l一β为直二面角，BD在β上，l=α∩β，BD⊥l，故BD⊥α．同理AC⊥β．
又∠BAD、∠ABC分别为AB与α、β所成的角，有∠BAD=x，∠ABC=y．
又EC∥BD，EC⊥l，AC⊥β，有AE⊥l，AE⊥BE，∠EBA=z．
∴cos2x+cos2y+sin2z=
| AD2 |
| AB2 |
| BC2 |
| AB2 |
| AE2 |
| AB2 |
故答案为：2
点评：本题的考点是与二面角有关的立体几何综合，主要考查线面角，线线角，考查求三角函数的值，关键是正确找出相应的角．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
相关题目
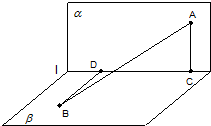（2006•广州一模）如图，长度为2的线段AB夹在直二面角α-l-β的两个半平面内，A∈α，B∈β，