题目内容
在△ABC中，给出如下命题：
①若
•
＞0，则△ABC为锐角三角形；
②O是△ABC所在平面内一定点，且满足
•
=
•
=
•
，则O是△ABC的垂心；
③O是△ABC所在平面内一定点，动点P满足
=
+λ(
+
)，λ∈[0，+∞)，则动点P一定过△ABC的重心；
④O是△ABC内一定点，且
+
+
=
，则
=
；
⑤若(
+
)•
=0，且
•
=
，则△ABC为等腰直角三角形．
其中正确的命题为
①若
| AC |
| AB |
②O是△ABC所在平面内一定点，且满足
| OA |
| OB |
| OB |
| OC |
| OC |
| OA |
③O是△ABC所在平面内一定点，动点P满足
| OP |
| OA |
| AB |
| AC |
④O是△ABC内一定点，且
| OA |
| OB |
| OC |
| 0 |
| S△AOC |
| S△ABC |
| 1 |
| 3 |
⑤若(
| ||
|
|
| ||
|
|
| BC |
| ||
|
|
| ||
|
|
| 1 |
| 2 |
其中正确的命题为
②③④
②③④
（将所有正确命题的序号都填上）．分析：①由数量积可以判断三角形的内角关系．②将向量进行化简，得到向量垂直关系．③将向量进行化简，得到向量共线关系．④将向量进行化简，得到向量共线关系，根据共线关系确定，O为重心．⑤利用平面向量的数量积公式，可推出向量垂直，进而判断三角形的边角关系．
解答：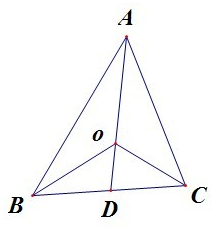
解：①若
•
＞0，则得出角A为锐角，但无法判断B，C都是锐角，所以①错误．
②由
?
=
?
，得(
-
)?
=0，即
?
=0，所以
⊥
．同理可知
⊥
，所以O是△ABC的垂心，所以②正确．
③由动点P满足
=
+λ(
+
)，λ∈[0，+∞)，
得
-
=λ(
+
)，即P的轨迹是直线AD，而AE是△ABC的中线，
因此P的轨迹（即直线AD）过△ABC的重心．所以③正确．
④由
+
+
=
，得
+
=-
=
在三角形ABC中，E是边BC的中点，则
=2
，即O是三角形ABC的重心，所以
=
，
=
，所以
=
×
=
×
=
，所以④正确．
⑤由(
+
)•
=0，可知角A的角平分线垂直于BC，所以AB=AC．由
•
=
，可得cos?A=
，解得
A=
，所以△ABC为等边三角形，所以⑤错误．所以正确的命题为②③④．
故答案为：②③④．
解：①若| AC |
| AB |
②由
| OA |
| OB |
| OB |
| OC |
| OA |
| OC |
| OB |
| AC |
| OB |
| AC |
| OB |
| AB |
| OC |
③由动点P满足
| OP |
| OA |
| AB |
| AC |
得
| OP |
| OA |
| AB |
| AC |
因此P的轨迹（即直线AD）过△ABC的重心．所以③正确．
④由
| OA |
| OB |
| OC |
| 0 |
| OC |
| OB |
| OA |
| AO |
| AO |
| OE |
| S△AOC |
| S△ADC |
| 2 |
| 3 |
| S△ADC |
| S△ABC |
| 1 |
| 2 |
| S△AOC |
| S△ABC |
| S△AOC |
| S△ADC |
| S△ADC |
| S△ABC |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
⑤由(
| ||
|
|
| ||
|
|
| BC |
| ||
|
|
| ||
|
|
| 1 |
| 2 |
| 1 |
| 2 |
A=
| π |
| 3 |
故答案为：②③④．
点评：本题主要考查平面向量数量积的应用，在做的过程中要利用数形结合的数学思想．
练习册系列答案
提分百分百检测卷系列答案
相关题目
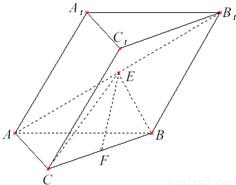
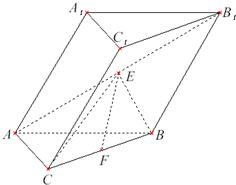如图，在斜三棱柱ABC-A1B1C1中，AC=BC，AC⊥BC．侧面A1ABB1是边长为a的菱形，且垂直于底面ABC，∠A1AB=60°，E，F分别是AB1，BC的中点． 
给出下列三个命题：
．
并使它与△ABC全等且A与A1是对应点；
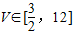，求a的取值范围．