题目内容
若斜率为2的动直线l与抛物线x2=4y相交于不同的两点A、B,O为坐标原点.(1)求线段AB中点P的轨迹方程;
(2)若
 ,求直线l在y轴上截距的取值范围.
,求直线l在y轴上截距的取值范围.
【答案】分析:(1)先把直线l的方程与抛物线的方程联立,求出点A、B之间的等量关系,再利用中点坐标公式即可求线段AB中点P的轨迹方程;(注意范围的限制)
(2)先利用(1)中求出的点A、B之间的等量关系,直接代入 ,即可求直线l在y轴上截距的取值范围.(注意范围的限制)
,即可求直线l在y轴上截距的取值范围.(注意范围的限制)
解答:解:(1)设l的方程为y=2x+b,l与C的交点坐标分别为A(x1,y1)、B(x2,y2),
点P(x,y),由 ,(2分)
,(2分)
得 ,依题意,
,依题意, (4分)
(4分)
故所求的轨迹方程为x=4(y>4).(7分)
(2)由(1)知 ,(2分)
,(2分)
由 得x1x2+y1y2=-4b+b2≤60(4分)
得x1x2+y1y2=-4b+b2≤60(4分)
解得-6≤b≤10(6分)注意到b>-4,
∴-4<b≤10.(7分)
点评:本题主要考查直线与抛物线的位置关系,向量的应用以及轨迹方程的求法,是对知识的综合考查,属于中档题目.在研究直线与圆锥曲线的位置关系时,一般常把直线与圆锥曲线方程联立,易错点在于忘记限制对应判别式.
(2)先利用(1)中求出的点A、B之间的等量关系,直接代入
 ,即可求直线l在y轴上截距的取值范围.(注意范围的限制)
,即可求直线l在y轴上截距的取值范围.(注意范围的限制)解答:解:(1)设l的方程为y=2x+b,l与C的交点坐标分别为A(x1,y1)、B(x2,y2),
点P(x,y),由
 ,(2分)
,(2分)得
 ,依题意,
,依题意, (4分)
(4分)故所求的轨迹方程为x=4(y>4).(7分)
(2)由(1)知
 ,(2分)
,(2分)由
 得x1x2+y1y2=-4b+b2≤60(4分)
得x1x2+y1y2=-4b+b2≤60(4分)解得-6≤b≤10(6分)注意到b>-4,
∴-4<b≤10.(7分)
点评:本题主要考查直线与抛物线的位置关系,向量的应用以及轨迹方程的求法,是对知识的综合考查,属于中档题目.在研究直线与圆锥曲线的位置关系时,一般常把直线与圆锥曲线方程联立,易错点在于忘记限制对应判别式.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
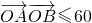 ,求直线l在y轴上截距的取值范围.
,求直线l在y轴上截距的取值范围.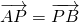 ,求动点P的轨迹方程;
,求动点P的轨迹方程;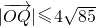 ,求直线l在y轴上截距的取值范围.
,求直线l在y轴上截距的取值范围.