题目内容
已知f(x)=3sin(2x+
)，则以下不等式正确的是（ ）
| π |
| 3 |
| A、f（3）＞f（1）＞f（2） |
| B、f（1）＞f（2）＞f（3） |
| C、f（3）＞f（2）＞f（1） |
| D、f（1）＞f（3）＞f（2） |
分析：结合正弦函数的图象，利用函数的单调性可知，f（3）＞0，f（1）＞0，f（2）＜0，在结合函数的图象，判断2与3距离对称轴的距离，从而判断f（1），f（3）的大小
解答：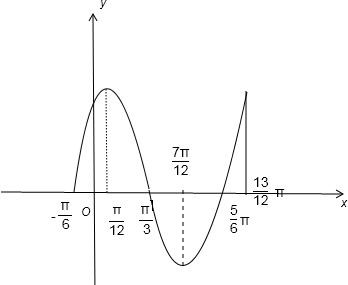
解：∵函数f(x)=3sin(2x+
)在[
，
]单调递减，在[
]单调递增
∵
＜1＜
，∴f（1）＞0
∵
＜2＜
＜3＜
，∴f（2）＜0，f（3）＞0
|
-3|＜|1-
|
∴3距对称轴比1距对称轴近
f（3）＞f（1）＞0＞f（2）
故选A．
解：∵函数f(x)=3sin(2x+| π |
| 3 |
| π |
| 12 |
| 7π |
| 12 |
| 7π |
| 12 |
| 13π |
| 12 |
∵
| π |
| 12 |
| π |
| 3 |
∵
| 7π |
| 12 |
| 5π |
| 6 |
| 13π |
| 12 |
，∴f（2）＜0，f（3）＞0
|
| 13π |
| 12 |
| π |
| 12 |
∴3距对称轴比1距对称轴近
f（3）＞f（1）＞0＞f（2）
故选A．
点评：本题主要考查了正弦函数的单调性及函数对称性质的应用，只要熟练掌握函数的图象并能灵活运用，就很容易解决问题．
练习册系列答案
备战中考寒假系列答案
相关题目