题目内容
【题目】已知函数f(x)=ln(ax+1)(x≥0,a>0), ![]() .
.
(1)讨论函数y=f(x)-g(x)的单调性;
(2)若不等式f(x)≥g(x)+1在x∈[0,+∞)时恒成立,求实数a的取值范围;
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)求导数可得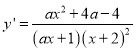 ,当
,当![]() 时,函数在
时,函数在![]() 上单调递增,当
上单调递增,当![]() 时,令
时,令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)由(1)知,当
的减区间;(2)由(1)知,当![]() 时,不等式
时,不等式![]() ,在
,在![]() 时恒成立,当
时恒成立,当![]() 时,可证明存在
时,可证明存在![]() 使得不等式
使得不等式![]() 不成立,综合可得
不成立,综合可得![]() 取值范围.
取值范围.
试题解析:(1)∵y=f(x)-g(x)=ln(ax+1)-![]() ,
,
y′=![]() -
-![]() =
=![]() ,
,
当a≥1时,y′≥0,所以函数y=f(x)-g(x)是[0,+∞)上的增函数;
当0<a<1时,由y′>0得x>2![]() ,所以函数y=f(x)-g(x)在
,所以函数y=f(x)-g(x)在![]() 上是单调递增函数,函数y=f(x)-g(x)在
上是单调递增函数,函数y=f(x)-g(x)在![]() 上是单调递减函数;
上是单调递减函数;
(2)当a≥1时,函数y=f(x)-g(x)是[0,+∞)上的增函数.
所以f(x)-g(x)≥f(0)-g(0)=1,
即不等式f(x)≥g(x)+1在x∈[0,+∞)时恒成立,
当0<a<1时,函数y=f(x)-g(x)是![]() 上的减函数,存在x0∈
上的减函数,存在x0∈![]() ,使得f(x0)-g(x0)<f(0)-g(0)=1,即不等式f(x0)≥g(x0)+1不成立,
,使得f(x0)-g(x0)<f(0)-g(0)=1,即不等式f(x0)≥g(x0)+1不成立,
综上,实数a的取值范围是[1,+∞).

练习册系列答案
相关题目
【题目】某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价为5元,销售单价与日均销售量的关系如图所示.
销售单价/元 | … | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | … |
日均销售量/桶 | … | 480 | 460 | 440 | 420 | 400 | 380 | … |
请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?