题目内容

【题目】已知，动点满足成等差数列。

（1）求点的轨迹方程；

（2）对于轴上的点，若满足，则称点为点对应的“比例点”，问：对任意一个确定的点，它总能对应几个“比例点”？

【答案】(1) (2) 对任意一个确定的点，它总能对应2个“比例点”

【解析】试题分析：(1)利用等差中项的定义可得利用双曲线定义写出轨迹方程即可；（2）考虑到在上，故可设出其坐标，设，写出｜｜、｜｜即，根据｜｜·｜｜＝计算得出关于的方程，判断此方程根的个数确定“比例点”.

试题解析：（1）由已知得

∴P点的轨迹是以A,B为焦点的双曲线的右支，且，

∴P点的轨迹方程为（标不扣分，不标扣1分） 5分

（2）设

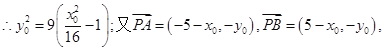
则

又

由得10分

，∴方程恒有两个不等实根

∴对任意一个确定的点P，它总能对应2个“比例点” 12分

练习册系列答案
相关题目

【题目】已知函数f（x）=|x﹣a|+|x+5﹣a|
（1）若不等式f（x）﹣|x﹣a|≤2的解集为[﹣5，﹣1]，求实数a的值；
（2）若x0∈R，使得f（x0）＜4m+m2 ， 求实数m的取值范围．

【题目】已知函数．

（）若关于的不等式的解集为，求实数的取值范围．

（）若关于的不等式的解集是，求，的值．

（）若关于的不等式的解集是，集合，若，求实数的取值范围．

【题目】双曲线的离心率为2，右焦点到它的一条渐近线的距离为 。

（1）求双曲线的标准方程；

（2）是否存在过点且与双曲线的右支角不同的两点的直线，当点满足时，使得点在直线上的射影点满足？若存在，求出直线的方程；若不存在，说明理由。

【题目】共享单车是城市交通的一道亮丽的风景,给人们短距离出行带来了很大的方便.某校”单车社团”对市年龄在岁骑过共享单车的人群随机抽取人调查,骑行者的年龄情况如下图显示。

（1）已知年龄段的骑行人数是两个年龄段的人数之和，请估计骑过共享单车人群的年齡的中位数；

（2）从两个年龄段骑过共享单车的人中按的比例用分层抽样的方法抽取人,从中任选人,求两人都在)的概率.

【题目】已知抛物线的焦点为，点在抛物线上，且。

（Ⅰ）求抛物线的标准方程及实数的值；

（Ⅱ）直线过抛物线的焦点，且与抛物线交于两点，若（为坐标原点）的面积为，求直线的方程.

【题目】矩形中， ， 边所在直线的方程为，点在边所在直线上．

（）求边所在直线的方程．

（）求矩形外接圆的方程．

（）若过点作题（）中的圆的切线，求切线的方程．

【题目】本着健康、低碳的生活理念，租自行车骑游的人越来越多．某自行车租车点的收费标准是每车每次租时间不超过两小时免费，超过两个小时的部分每小时收费2元（不足1小时的部分按 1小时计算）．有甲、乙两人独立来该租车点租车骑游（各租一车一次）．设甲、乙不超过两小时还车的概率分别为；两小时以上且不超过三小时还车的概率分别为；两人租车时间都不会超过四小时．

（1）求甲、乙两人所付租车费用相同的概率；

（2）设甲、乙两人所付的租车费用之和为随机变量，求的分布列．

【题目】（本题满分12分）甲、乙两位学生参加数学竞赛培训，现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次，记录如下：

甲 82 81 79 78 95 88 93 84

乙 92 95 80 75 83 80 90 85

（1）用茎叶图表示这两组数据；

（2）现要从中选派一人参加数学竞赛，从统计学的角度（在平均数、方差或标准差中选两个）分析，你认为选派哪位学生参加合适？请说明理由

参考公式：

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网