题目内容
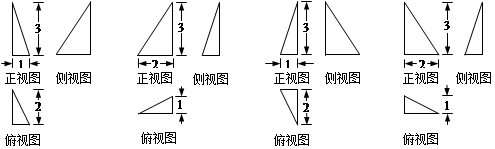
已知一个几何体的主视图及左视图均是边长为2的正三角形,俯视图是直径为2的圆,则此几何体的外接球的体积为( )
A.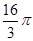 | B. | C. | D. |
C
解析试题分析:该几何体为圆锥。设该圆锥的外接球的球心为O,半径为R,球心O到圆锥底面的距离为x,则可得到 ,解之得R=
,解之得R= ,
,
所以此几何体的外接球的体积=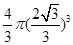 =
= .选C。
.选C。
考点:三视图,圆锥及其外接球的几何特征,球的体积。
点评:中档题,三视图与圆锥、球综合考查,难度较之于高考题大了些。注意掌握三视图画法规则,正确还原几何体,注意将空间问题转化成平面问题。

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
已知圆柱 底面半径为1,高为
底面半径为1,高为 ,
, 是圆柱的一个轴截面.动点
是圆柱的一个轴截面.动点 从点
从点 出发沿着圆柱的侧面到达点
出发沿着圆柱的侧面到达点 ,其距离最短时在侧面留下的曲线
,其距离最短时在侧面留下的曲线 如图所示.
如图所示.
现将轴截面 绕着轴
绕着轴 逆时针旋转
逆时针旋转 后,边
后,边 与曲线
与曲线 相交于点
相交于点 ,设
,设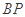 的长度为
的长度为 ,则
,则 的图象大致为( )
的图象大致为( )
某几何体的三视图如图所示,则该几何体的体积不可能是
A. | B. |
C. | D. |
某个几何体的三视图如图所示,其中俯视图为等边三角形,则该几何体的表面积是( )
A. | B. |
C.6+ | D. |
一个三棱锥的三视图如图所示,则该几何体的表面积为( )
A. | B. |
C. | D.8 |
图中最左边的几何体由一个圆柱挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得.现用一个竖直的平面去截这个几何体,则截面图形可能是 ( )

| A.(1)(2) | B.(1)(3) | C.(1)(4) | D.(1)(5) |

 长为2;侧视图一直角三角形;俯视图为一直角梯形,且
长为2;侧视图一直角三角形;俯视图为一直角梯形,且 ,则此几何体的体积是( )。
,则此几何体的体积是( )。