Question

若实数x，y满足

x+3y-3≤0 x≥0 y≥0

，则目标函数z=x²+（y-2）²的最大值是

13

．

Answer 1

分析：画出满足条件的可行域，分析出目标函数z=x²+（y-2）²表示可行域内一点（x，y）到点（0，2）点距离的平方，数形结合分析出可行域上到（0，2）点距离最远的点，代入可得目标函数的最大值．

解答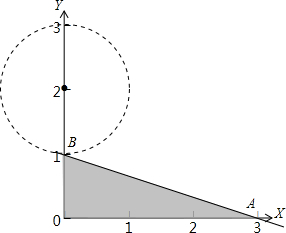：解：满足

x+3y-3≤0 x≥0 y≥0

的可行域如下图中阴影部分所示：
目标函数z=x²+（y-2）²表示可行域内一点（x，y）到点（0，2）点距离的平方
由图可得B到（0，1）点距离最近，此时z=x²+（y-2）²=1
A到（0，1）点距离最远，此时z=x²+（y-2）²=13
即目标函数z=x²+（y-2）²的最大值是13
故答案为：13

点评：本题考查的知识点是线性规划的应用，其中分析出目标函数的几何意义是解答的关键．