题目内容
(本小题满分12分)
设函数![]()
(Ⅰ)当![]() 时,求
时,求![]() 的最大值;
的最大值;
(Ⅱ)令![]() ,(
,(![]() ),其图象上任意一点
),其图象上任意一点![]() 处切线的斜率
处切线的斜率![]() ≤
≤![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() ,
,![]() ,方程
,方程![]() 有唯一实数解,求正数
有唯一实数解,求正数![]() 的值.
的值.
解: (Ⅰ)依题意,知![]() 的定义域为(0,+∞),
的定义域为(0,+∞),
当![]() 时,
时,![]() ,
,
![]() (2′)令
(2′)令![]() =0,
=0,
解得![]() .(∵
.(∵![]() )
)
因为![]() 有唯一解,所以
有唯一解,所以![]() ,当
,当![]() 时,
时,
![]() ,此时
,此时![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,此时
,此时![]() 单调递减。
单调递减。
所以![]() 的极大值为
的极大值为![]() ,此即为最大值 ………4分
,此即为最大值 ………4分
(Ⅱ)![]() ,
,![]() ,则有
,则有![]() ≤
≤![]() ,在
,在![]() 上恒成立,
上恒成立,
所以![]() ≥
≥![]() ,
,![]()
当![]() 时,
时,![]() 取得最大值
取得最大值![]() ,所以
,所以![]() ≥
≥![]() ………8分
………8分
(Ⅲ)因为方程![]() 有唯一实数解,
有唯一实数解,
所以![]() 有唯一实数解,
有唯一实数解,
设![]() ,
,
则![]() .令
.令![]() ,
,![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() (舍去),
(舍去),![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在(0,
在(0,![]() )上单调递减,
)上单调递减,
当![]() 时,
时,![]() ,
,![]() 在(
在(![]() ,+∞)单调递增
,+∞)单调递增
当![]() 时,
时,![]() =0,
=0,![]() 取最小值
取最小值![]() .
.
则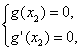 既
既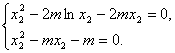
所以![]() ,因为
,因为![]() ,所以
,所以![]() (*)
(*)
设函数![]() ,因为当
,因为当![]() 时,
时,
![]() 是增函数,所以
是增函数,所以![]() 至多有一解.
至多有一解.
因为![]() ,所以方程(*)的解为
,所以方程(*)的解为![]() ,即
,即![]() ,解得
,解得![]() .…12分
.…12分

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目