题目内容
(本小题满分12分)
设二次函数f(x)=ax2+bx(a≠0)满足条件:
①f(-1+x)=f(-1-x);②函数f(x)的图象与直线y=x只有一个公共点.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若不等式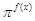 >(
>(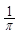 )2-tx在t∈[-2,2]时恒成立,求实数x的取值范围.
)2-tx在t∈[-2,2]时恒成立,求实数x的取值范围.
【答案】
(Ⅰ) 函数 的解析式为
的解析式为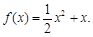
(Ⅱ)实数 的取值范围是
的取值范围是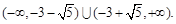
【解析】解:(Ⅰ) 由①知
由①知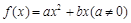 的对称轴方程是
的对称轴方程是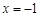 ,
,
 ;……………………………………………………………………………1分
;……………………………………………………………………………1分
 函数
函数 的图象与直线
的图象与直线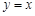 只有一个公共点,
只有一个公共点,
 方程组
方程组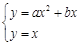 有且只有一解,即
有且只有一解,即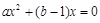 有两个相同的实根;
有两个相同的实根;
 Δ=
Δ=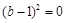 ,即
,即 ,
, ………………………………………3分
………………………………………3分
 函数
函数 的解析式为
的解析式为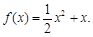 …………………………………………4分
…………………………………………4分
(Ⅱ)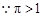 ,
,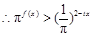 等价于
等价于 ,…………………………6分
,…………………………6分
 在
在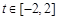 时恒成立等价于
时恒成立等价于
函数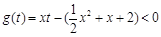 在
在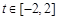 时恒成立;……………………9分
时恒成立;……………………9分
 ,即
,即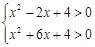 ,
,
解得: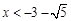 或
或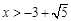 ,
,
综上:实数 的取值范围是
的取值范围是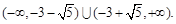 ………………………12分
………………………12分

练习册系列答案
相关题目