题目内容
给出下列命题:
(1)存在实数α,使sinαcosα=1;
(2)存在实数α,使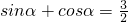 ;
;
(3)函数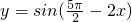 是偶函数;
是偶函数;
(4)方程 是函数
是函数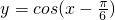 图象的一条对称轴方程;
图象的一条对称轴方程;
(5)若α,β是第一象限角,且α>β,则tanα>tanβ.
(6)把函数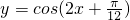 的图象向右平移
的图象向右平移 个单位,所得的函数解析式为
个单位,所得的函数解析式为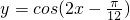
其中正确命题的序号是 ________.(注:把你认为正确的命题的序号都填上)
解(1)sinαcosα=1? sin2α=1?sin2α=2>1故(1)错误
sin2α=1?sin2α=2>1故(1)错误
(2)sinα+cosα= ?
? ?sin
?sin >1故(2)错误
>1故(2)错误
(3) 是偶函数,故(3)正确
是偶函数,故(3)正确
(4)y=cos(x- )的对称轴是x-
)的对称轴是x- =kπ?x=
=kπ?x= +kπ(,k∈Z)故(4)正确
+kπ(,k∈Z)故(4)正确
(5)例如:β=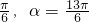 ,而tanα=tanβ故(5)错误
,而tanα=tanβ故(5)错误
(6)把函数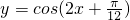 的图象向右平移
的图象向右平移 个单位,所得的函数解析式为y=cos[2(x-
个单位,所得的函数解析式为y=cos[2(x- )+
)+ ]即为
]即为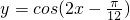 ,故(6)正确
,故(6)正确
故答案为:(3)(4)(6)
分析:(1)利用二倍角公式可得sin2α=2>1,(2)利用两角和的正弦公式可得, (3)先利用诱导公式化简,然后根据偶函数的定义判断(4)求出函数的对称轴,把
(3)先利用诱导公式化简,然后根据偶函数的定义判断(4)求出函数的对称轴,把 代入检验(5)举反例
代入检验(5)举反例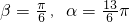 (6)根据函数的平移法则左加右减可得.
(6)根据函数的平移法则左加右减可得.
点评:本题综合考查了三角函数的二倍角公式,两角和的正弦公式,正弦函数的值域-1≤sinx≤1,正余弦函数的对称性,函数平移法则.解决本题的关键是熟练的掌握三角函数的相关性质,灵活运用性质.
 sin2α=1?sin2α=2>1故(1)错误
sin2α=1?sin2α=2>1故(1)错误(2)sinα+cosα=
 ?
? ?sin
?sin >1故(2)错误
>1故(2)错误(3)
 是偶函数,故(3)正确
是偶函数,故(3)正确(4)y=cos(x-
 )的对称轴是x-
)的对称轴是x- =kπ?x=
=kπ?x= +kπ(,k∈Z)故(4)正确
+kπ(,k∈Z)故(4)正确(5)例如:β=
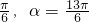 ,而tanα=tanβ故(5)错误
,而tanα=tanβ故(5)错误(6)把函数
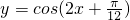 的图象向右平移
的图象向右平移 个单位,所得的函数解析式为y=cos[2(x-
个单位,所得的函数解析式为y=cos[2(x- )+
)+ ]即为
]即为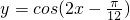 ,故(6)正确
,故(6)正确故答案为:(3)(4)(6)
分析:(1)利用二倍角公式可得sin2α=2>1,(2)利用两角和的正弦公式可得,
 (3)先利用诱导公式化简,然后根据偶函数的定义判断(4)求出函数的对称轴,把
(3)先利用诱导公式化简,然后根据偶函数的定义判断(4)求出函数的对称轴,把 代入检验(5)举反例
代入检验(5)举反例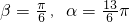 (6)根据函数的平移法则左加右减可得.
(6)根据函数的平移法则左加右减可得.点评:本题综合考查了三角函数的二倍角公式,两角和的正弦公式,正弦函数的值域-1≤sinx≤1,正余弦函数的对称性,函数平移法则.解决本题的关键是熟练的掌握三角函数的相关性质,灵活运用性质.

练习册系列答案
相关题目