题目内容
(1)设关于x的不等式
>0的解集为P,若P={x|-3<x<-1},求实数a的值;
(2)已知函数f(x)=|x-2|+|x-4|解不等式f(x)≤4.
| ax-1 | x+1 |
(2)已知函数f(x)=|x-2|+|x-4|解不等式f(x)≤4.
分析:(Ⅰ)由
>0的解集为P={x|-3<x<-1},可得-3和-1是不等式中各个因式的根,故
=-3,由此求得a的值.
(Ⅱ)要解的不等式即 ①
,或 ②
,或③
.分别求出①、②、③的解集,再取并集,即得所求.
| ax-1 |
| x+1 |
| 1 |
| a |
(Ⅱ)要解的不等式即 ①
|
|
|
解答: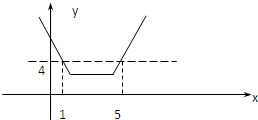 解:(Ⅰ)由
解:(Ⅰ)由
>0的解集为P={x|-3<x<-1},可得-3和-1是不等式中各个因式的根,故
=-3,
∴a=-
. …(5分)
(Ⅱ)f(x)=|x-2|+|x-4|=
…(7分)
故要解的不等式即 ①
,或 ②
,或③
.
解①得1≤x≤2,解②得 2 x<4,解③得 4≤x≤5.….(10分)
综上可得,不等式的解集为:{x|1≤x≤5}.…(12分)
 解:(Ⅰ)由
解:(Ⅰ)由| ax-1 |
| x+1 |
| 1 |
| a |
∴a=-
| 1 |
| 3 |
(Ⅱ)f(x)=|x-2|+|x-4|=
|
故要解的不等式即 ①
|
|
|
解①得1≤x≤2,解②得 2 x<4,解③得 4≤x≤5.….(10分)
综上可得,不等式的解集为:{x|1≤x≤5}.…(12分)
点评:本题主要考查绝对值不等式的解法,分式不等式的解法,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
 (2012•盐城二模)因客流量临时增大,某鞋店拟用一个高为50cm(即EF=50cm)的平面镜自制一个竖直摆放的简易鞋镜.根据经验,一般顾客AB的眼睛B到地面的距离x(cm)在区间[140,180]内.设支架FG高为h(0<h<90)cm,AG=100cm,顾客可视的镜像范围为CD(如图所示),记CD的长度为y(y=GD-GC).
(2012•盐城二模)因客流量临时增大,某鞋店拟用一个高为50cm(即EF=50cm)的平面镜自制一个竖直摆放的简易鞋镜.根据经验,一般顾客AB的眼睛B到地面的距离x(cm)在区间[140,180]内.设支架FG高为h(0<h<90)cm,AG=100cm,顾客可视的镜像范围为CD(如图所示),记CD的长度为y(y=GD-GC).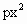 +(p-1)x+p+1=0有两个不等的正根,且一根大于另一根的两倍,求p的取值范围.
+(p-1)x+p+1=0有两个不等的正根,且一根大于另一根的两倍,求p的取值范围.