题目内容
如图所示,已知AB为圆O的直径,点D为线段AB上一点,且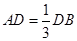 ,点C为圆O上一点,且
,点C为圆O上一点,且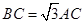 .点P在圆O所在平面上的正投影为点D,PD=DB.
.点P在圆O所在平面上的正投影为点D,PD=DB.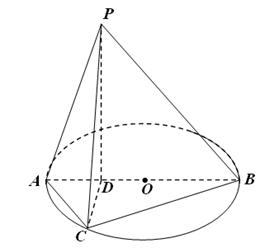
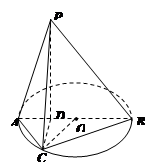
(1)求证: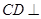 平面
平面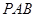 ;
;
(2)求点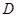 到平面
到平面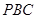 的距离.
的距离.
(1)证明见解析;(2) 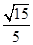 .
.
解析试题分析:(1)先利用平面几何知识与线面垂直的性质证线线垂直,由线线垂直得到线面垂直,再由线面垂直得到线线垂直;(2)点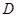 到平面
到平面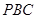 的距离是棱锥D-PCB顶点D到底面的高,求出棱锥的体积和底面三角形PCB的面积,可以求出点
的距离是棱锥D-PCB顶点D到底面的高,求出棱锥的体积和底面三角形PCB的面积,可以求出点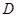 到平面
到平面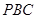 的距离.
的距离.
试题解析:(1)如图,连接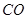 ,
,
由3AD=DB知,点D为AO的中点,
又∵AB为圆O的直径,
∴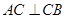 ,
,
由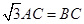 知,
知,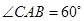 ,
,
∴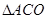 为等边三角形,
为等边三角形,
故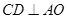 .
.
∵点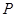 在圆
在圆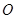 所在平面上的正投影为点
所在平面上的正投影为点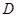 ,
,
∴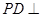 平面
平面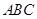 ,
,
又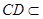 平面
平面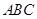 ,
,
∴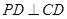 ,
,
由PDÌ平面PAB,AOÌ平面PAB,且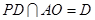 ,
,
得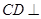 平面
平面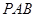 .
.
(2)由(1)可知 ,
,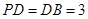 ,
,
∴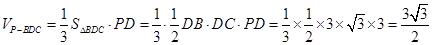 ,
,
又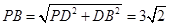 ,
,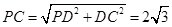 ,
,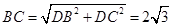 ,
,
∴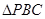 为等腰三角形,则
为等腰三角形,则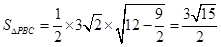 ,
,
设点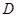 到平面
到平面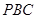 的距离为
的距离为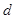 ,
,
由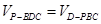 得,
得,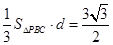 ,
,
解得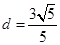 .
.
考点:1.直线与平面垂直的判定;2.点到平面距离.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 中,
中,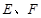 分别为
分别为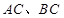 的中点.
的中点.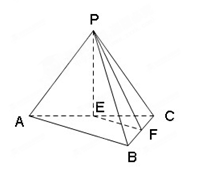
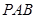 ;
;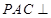 平面
平面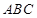 ,且
,且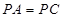 ,
,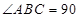 º,求证:平面
º,求证:平面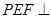 平面
平面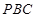
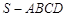 ,底面
,底面 为平行四边形,侧面
为平行四边形,侧面 底面
底面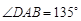 ,
,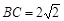 ,
,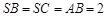 ,
,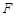 为线段
为线段 的中点.
的中点.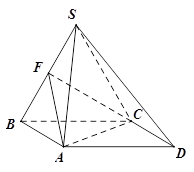
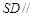 平面
平面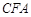 ;
; 与面
与面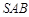 所成二面角大小.
所成二面角大小.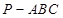 中,
中,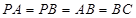 ,
,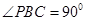 ,D为AC的中点,
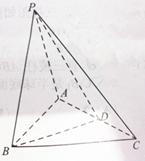
,D为AC的中点,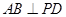 .
.
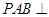 平面
平面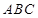 ;
;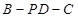 的余弦值.
的余弦值.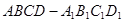 中,
中, ,
,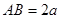 , E、
, E、  分别为
分别为 、
、 的中点.
的中点.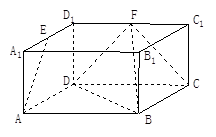
 平面
平面 ;
;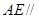 平面
平面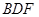 .
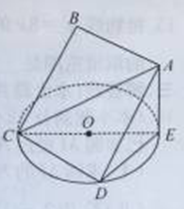
.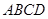 所在平面与圆
所在平面与圆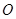 所在的平面相交于
所在的平面相交于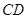 ,线段
,线段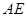 垂直于圆
垂直于圆 为圆
为圆 、
、 的点,设正方形
的点,设正方形 ,且
,且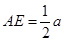 .
.
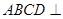 平面
平面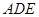 ;
;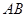 与
与 所成的角为
所成的角为 ,
,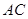 与底面
与底面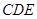 所成角为
所成角为 ,二面角
,二面角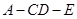 所成角为
所成角为 ,求证
,求证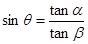
 ,直线B1C与平面ABC成45°角.
,直线B1C与平面ABC成45°角.
 中,已知平面
中,已知平面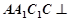 平面
平面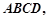 且
且 ,
, .
.

 为棱
为棱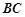 的中点,求证:
的中点,求证: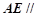 平面
平面 .
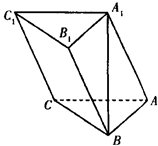
. 中,
中,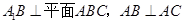 .
.
 ;
; ,在棱
,在棱 上确定一点P, 使二面角
上确定一点P, 使二面角 的平面角的余弦值为
的平面角的余弦值为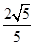 .
.