题目内容
对正整数n≥2,记an=
•
(1)求a2,a3,a4,a5的值;
(2)求证:当n≥5时,有an≤
.
| n-1 |
 |
| i=1 |
| n |
| n-i |
| 1 |
| 2i-1 |
(1)求a2,a3,a4,a5的值;
(2)求证:当n≥5时,有an≤
| 10 |
| 3 |
分析:(1)由于an=
•
,将n=2,3,4,5代入计算即可求得a2,a3,a4,a5的值;
(2)利用数学归纳法,①当n≤5时,由(1)的结论可判断所证关系式是否成立;②假设n=k时,结论成立,去推证n=k+1时,命题亦成立即可.
| n-1 |
 |
| i=1 |
| n |
| n-i |
| 1 |
| 2i-1 |
(2)利用数学归纳法,①当n≤5时,由(1)的结论可判断所证关系式是否成立;②假设n=k时,结论成立,去推证n=k+1时,命题亦成立即可.
解答:解:(1)依题意,a2=
•
=2
同理可得a3=3,a4=a5=
,---------------------(4分)
(2)下面用数学归纳法证明:当n≥5时,有an≤
.
①当n≤5时,由(1)可得an≤
;
②假设n=k时,ak≤
(k≥5),
则n=k+1时,ak+1=
+
×
+
×
+…+
×
---------(6分)
=
+
(
+
×
+…+
×
)
=
+
ak---------------------------------(8分)
≤
+
×
=
×
≤
×
=
<
.
所以当n=k+1时命题成立
综上,当n≥5时,有an≤
.----------------------------------------------(10分)
| 2 |
| 2-1 |
| 1 |
| 21-1 |
同理可得a3=3,a4=a5=
| 10 |
| 3 |
(2)下面用数学归纳法证明:当n≥5时,有an≤
| 10 |
| 3 |
①当n≤5时,由(1)可得an≤
| 10 |
| 3 |
②假设n=k时,ak≤
| 10 |
| 3 |
则n=k+1时,ak+1=
| k+1 |
| k |
| k+1 |
| k-1 |
| 1 |
| 2 |
| k+1 |
| k-2 |
| 1 |
| 22 |
| k+1 |
| 1 |
| 1 |
| 2k-1 |
=
| k+1 |
| k |
| k+1 |
| 2k |
| k |
| k-1 |
| k |
| k-2 |
| 1 |
| 2 |
| k |
| 1 |
| 1 |
| 2k-2 |
=
| k+1 |
| k |
| k+1 |
| 2k |
≤
| k+1 |
| k |
| 10 |
| 3 |
| k+1 |
| 2k |
=
| k+1 |
| k |
| 8 |
| 3 |
≤
| 6 |
| 5 |
| 8 |
| 3 |
| ||
| 3 |
| 10 |
| 3 |
所以当n=k+1时命题成立
综上,当n≥5时,有an≤
| 10 |
| 3 |
点评:本题考查数学归纳法,考查运算与等价转化思想、考查推理分析与论证的能力,属于难题.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
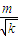 |m∈In,k∈In}.
|m∈In,k∈In}.