题目内容
[2014·福建调研]若点O和点F分别为椭圆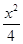 +
+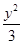 =1的中心和左焦点,点P为椭圆上的任意一点,则
=1的中心和左焦点,点P为椭圆上的任意一点,则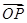 ·
·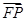 的最大值为( )
的最大值为( )
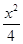 +
+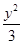 =1的中心和左焦点,点P为椭圆上的任意一点,则
=1的中心和左焦点,点P为椭圆上的任意一点,则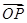 ·
·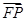 的最大值为( )
的最大值为( )| A.2 | B.3 | C.6 | D.8 |
C
由椭圆方程得F(-1,0),设P(x0,y0),则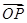 ·
·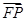 =(x0,y0)·(x0+1,y0)=x02+x0+y02.
=(x0,y0)·(x0+1,y0)=x02+x0+y02.
∵P为椭圆上一点,∴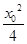 +
+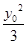 =1.
=1.
∴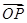 ·
·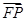 =x02+x0+3(1-
=x02+x0+3(1-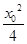 )
)
=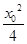 +x0+3=
+x0+3=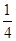 (x0+2)2+2.
(x0+2)2+2.
∵-2≤x0≤2,
∴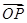 ·
·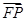 的最大值在x0=2时取得,且最大值等于6.
的最大值在x0=2时取得,且最大值等于6.
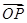 ·
·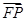 =(x0,y0)·(x0+1,y0)=x02+x0+y02.
=(x0,y0)·(x0+1,y0)=x02+x0+y02.∵P为椭圆上一点,∴
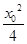 +
+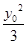 =1.
=1.∴
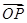 ·
·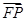 =x02+x0+3(1-
=x02+x0+3(1-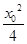 )
)=
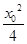 +x0+3=
+x0+3=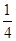 (x0+2)2+2.
(x0+2)2+2.∵-2≤x0≤2,
∴
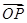 ·
·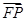 的最大值在x0=2时取得,且最大值等于6.
的最大值在x0=2时取得,且最大值等于6.
练习册系列答案
相关题目
 中,
中, 分别是与x轴,y轴平行的单位向量,若直角三角形ABC中,
分别是与x轴,y轴平行的单位向量,若直角三角形ABC中, ,则实数m=________________.
,则实数m=________________.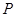 是椭圆
是椭圆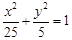 上一点,
上一点,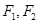 是椭圆的两个焦点,
是椭圆的两个焦点,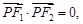
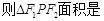 ( )
( )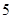
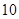
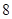
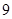
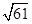 ,则a与b的夹角θ=( )
,则a与b的夹角θ=( ) 的部分图象如下图所示,则
的部分图象如下图所示,则 ( )
( )
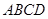 中,
中,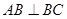 ,
,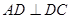 .若
.若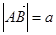 ,
,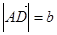 ,则
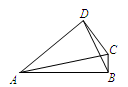
,则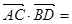 ()
()
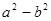
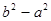
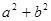
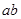
 ,向量
,向量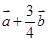 与
与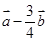 的位置关系为( )
的位置关系为( )
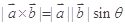 ,其中
,其中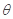 为向量
为向量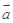 与
与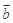 的夹角,若
的夹角,若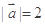 ,
,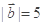 ,
,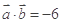 ,则
,则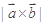 等于 ( )
等于 ( )