题目内容
已知矩阵M＝
.
(1)求矩阵M的逆矩阵；
(2)求矩阵M的特征值及特征向量．
（1）
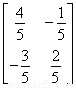（2）
【解析】(1)设M－1＝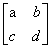
.
则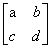
＝
＝
，
∴
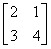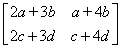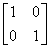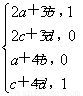解得
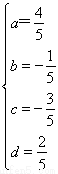∴M－1＝.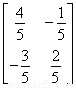
(2)矩阵A的特征多项式为f(x)＝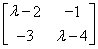
＝(λ－2)·(λ－4)－3＝
λ2－6λ＋5，令f(λ)＝0，
得矩阵M的特征值为1或5，当λ＝1时，由二元一次方程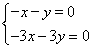
得x＋y＝0，令x＝1，则y＝－1，所以特征值λ＝1对应的特征向量为α1＝
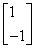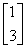
；当λ＝5时，由二元一次方程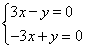
得3x－y＝0，令x＝1，则y＝3，所以特征值λ＝5对应的特征向量为α2＝
练习册系列答案
相关题目
