题目内容
根据下面各数列前几项的值,写出数列的一个通项公式:
(1)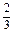 ,
,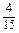 ,
,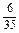 ,
,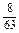 ,
,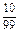 ,…
,…
(2)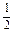 ,2,
,2,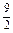 ,8,
,8,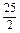 ,…
,…
(3)5,55,555,5 555,55 555,…
(4)5,0,-5,0,5,0,-5,0,…
(5)1,3,7,15,31,…
(1)
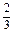 ,
,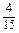 ,
,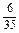 ,
,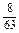 ,
,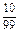 ,…
,…(2)
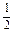 ,2,
,2,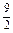 ,8,
,8,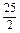 ,…
,…(3)5,55,555,5 555,55 555,…
(4)5,0,-5,0,5,0,-5,0,…
(5)1,3,7,15,31,…
(1)an=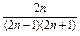 .(2)an=
.(2)an=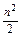 .(3)an=
.(3)an=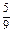 (10n-1).(4)an=5sin
(10n-1).(4)an=5sin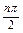 .(5)an=2n-1
.(5)an=2n-1
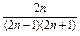 .(2)an=
.(2)an=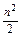 .(3)an=
.(3)an=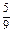 (10n-1).(4)an=5sin
(10n-1).(4)an=5sin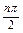 .(5)an=2n-1
.(5)an=2n-1(1)这是一个分数数列,其分子构成偶数数列,而分母可分解成1×3,3×5,5×7,7×9,9×11,…,每一项都是两个相邻奇数的乘积,经过组合,则所求数列的通项公式
an=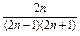 .
.
(2)数列的项,有的是分数,有的是整数,可将数列的各项都统一成分数再观察: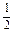 ,
,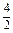 ,
,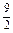 ,
,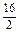 ,
,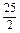 ,…,
,…,
可得通项公式an=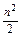 .
.
(3)联想 =10n-1,
=10n-1,
则an=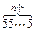 =
=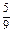
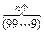 =
=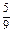 (10n-1),
(10n-1),
即an=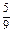 (10n-1).
(10n-1).
(4)数列的各项都具有周期性,联想基本数列1,0,-1,0,…,
则an=5sin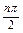 .
.
(5)∵1=2-1,3=22-1,7=23-1,…
∴an=2n-1
故所求数列的通项公式为an=2n-1.
an=
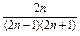 .
.(2)数列的项,有的是分数,有的是整数,可将数列的各项都统一成分数再观察:
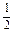 ,
,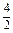 ,
,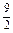 ,
,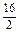 ,
,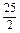 ,…,
,…,可得通项公式an=
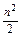 .
.(3)联想
 =10n-1,
=10n-1,则an=
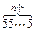 =
=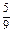
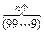 =
=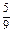 (10n-1),
(10n-1),即an=
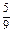 (10n-1).
(10n-1).(4)数列的各项都具有周期性,联想基本数列1,0,-1,0,…,
则an=5sin
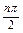 .
.(5)∵1=2-1,3=22-1,7=23-1,…
∴an=2n-1
故所求数列的通项公式为an=2n-1.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 满足:
满足: ,
, ,则
,则 ( )
( )


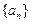 中,
中, N*,则
N*,则 ( )
( )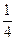



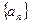 中,
中,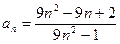 .
.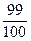 是否为该数列的项,为什么?
是否为该数列的项,为什么?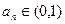 ;
; 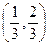 内有无数列的项,若有,有几项?若无,说明理由.
内有无数列的项,若有,有几项?若无,说明理由. ,满足
,满足 , 且
, 且 , 则
, 则 = 。
= 。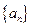 ,已知
,已知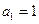 ,当
,当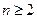 时
时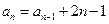 ,依次计算
,依次计算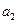 、
、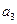 、
、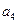 后,猜想
后,猜想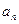 的表达式是( )
的表达式是( )




 ,
, ,那么
,那么 是这个数列的第 项.
是这个数列的第 项.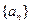 对任意的正整数n,都有
对任意的正整数n,都有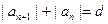 (d为常数),则称
(d为常数),则称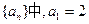 ,“绝对公和”
,“绝对公和”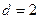 ,则其前2010项和
,则其前2010项和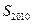 的最小值为( )
的最小值为( ) 成等比数列,则方程
成等比数列,则方程 的根有 个.
的根有 个.