题目内容
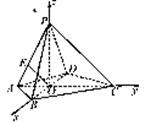
(本小题满分12分)如图,在四边形ABCD中,AC⊥BD,垂足为O,PO⊥平面ABCD,AO=BO=DO=1,CO=PO=2,E是线段PA上的点,AE∶AP=1∶3.
(1) 求证:OE∥平面PBC;
(2) 求二面角D-PB-C的大小.

【答案】
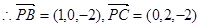 …………7分
…………7分
(1)略
(2)二面角D—PB—C的大小为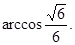
【解析】解:(I)由题意AO=1,AC=3,∴AO:AC=1:3
又AE:AP=1:3
∴在 中,OE//PC。 …………3分
中,OE//PC。 …………3分
又OE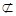 平面PBC,
平面PBC,
∴OE//平面PBC。 …………6分
(II)如图建立空间直角坐标系O—xyz,由已知
B(1,0,0),C(0,2,0),D(-1,0,0),P(0,0,2)
|
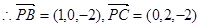 …………7分
…………7分
设平面PBC的法向量为 ,则
,则

得n=(2,1,1) …………9分
设平面PBD的法向量为m=(0,1,0) …………10分

∵二面角D—PB—C为锐二面角,
∴二面角D—PB—C的大小为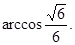 …………12分
…………12分

练习册系列答案
相关题目