题目内容
若正数 满足
满足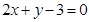 ,则
,则 的最小值为 .
的最小值为 .
3
解析试题分析:由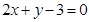 ,得
,得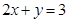 ,又∵
,又∵ 为正数,所以
为正数,所以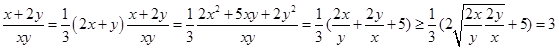 ,当且仅当
,当且仅当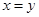 时取等号,因为
时取等号,因为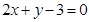 ,所以此时
,所以此时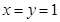 ,所以
,所以 的最小值为3,故答案为3.
的最小值为3,故答案为3.
考点:基本不等式.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
题目内容
若正数 满足
满足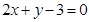 ,则
,则 的最小值为 .
的最小值为 .
3
解析试题分析:由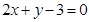 ,得
,得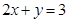 ,又∵
,又∵ 为正数,所以
为正数,所以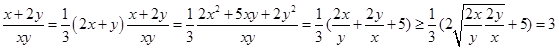 ,当且仅当
,当且仅当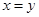 时取等号,因为
时取等号,因为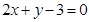 ,所以此时
,所以此时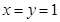 ,所以
,所以 的最小值为3,故答案为3.
的最小值为3,故答案为3.
考点:基本不等式.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案