题目内容
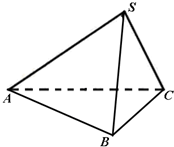
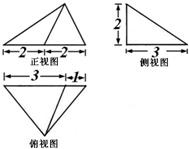 一个三棱锥S-ABC的三视图、直观图如图.
一个三棱锥S-ABC的三视图、直观图如图.(1)求三棱锥S-ABC的体积;
(2)求点C到平面SAB的距离;
(3)求二面角S-AB-C的余弦值.
分析:(1)由已知中的三视图,我们可以判断出已知三棱锥B在平面SAC上的正投影为AC的中点D,点S在平面ABC上的正投影为DC的中点O,进而我们求出底面ABC的面积和高SO的长,代入棱锥体积公式即可得到答案.
(2)解法一:以O为原点,OA为x轴,过O且平行于BD的直线为y轴,OS为z轴,建立如图空间直角坐标系,求出面SAB的一个法向量
,代入公式d=|
|,即可求出点C到平面SAB的距离;
解法二:设点C到平面SAB的距离为d,由三棱锥S-ABC的体积4=VS-ABC=VC-SAB=
×S△SAB×d,即可得到点C到平面SAB的距离;
(3)解法一:求出平面ABC一个法向量
,结合(2)中面SAB的一个法向量
,代入向量夹角公式,即可得到二面角S-AB-C的余弦值.
解法二:作CH⊥AB于H,作OE∥CH交AB于E,则OE⊥AB,连接SE,因OE是SE在底面ABC内的射影,而OE⊥AB,故SE⊥AB,∠SEO为二面角S-AB-C的平面角.解Rt△SEO即可得到到二面角S-AB-C的余弦值.
(2)解法一:以O为原点,OA为x轴,过O且平行于BD的直线为y轴,OS为z轴,建立如图空间直角坐标系,求出面SAB的一个法向量
| m |
| ||||
|
解法二:设点C到平面SAB的距离为d,由三棱锥S-ABC的体积4=VS-ABC=VC-SAB=
| 1 |
| 3 |
(3)解法一:求出平面ABC一个法向量
| n |
| m |
解法二:作CH⊥AB于H,作OE∥CH交AB于E,则OE⊥AB,连接SE,因OE是SE在底面ABC内的射影,而OE⊥AB,故SE⊥AB,∠SEO为二面角S-AB-C的平面角.解Rt△SEO即可得到到二面角S-AB-C的余弦值.
解答: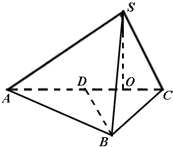 解:(1)由正视图、俯视图知AC=4;
解:(1)由正视图、俯视图知AC=4;
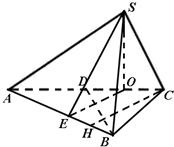
由正视图、侧视图知,点B在平面SAC上的正投影为AC的中点D,则BD=3,BD⊥平面SAC,BD⊥AC;
由俯视图、侧视图知,点S在平面ABC上的正投影为DC的中点O,
则SO=2,SO⊥平面ABC,SO⊥AC.如图.
三棱锥S-ABC的体积VS-ABC=
×(
×4×3)×2=4.
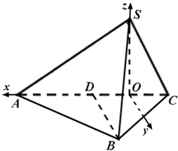
(2)解法一:
以O为原点,OA为x轴,过O且平行于BD的直线为y轴,OS为z轴,建立如图空间直角坐标系,可求S(0,0,2)A(3,0,0)B(1,3,0),
=(3,0,-2),
=(1,3,-2),
设
=(x,y,z)是平面SAB的一个法向量,则
,取
=(3,2,
),
可知C(-1,0,0),
=(4,0,0),设点C到平面SAB的距离为d,
则d=|
|=
.
(2)解法二:可求AB=
=
,SA=
=
,SB=
=
=
,
△SAB的面积S△SAB=
×
×
=
,
设点C到平面SAB的距离为d,
由三棱锥S-ABC的体积4=VS-ABC=VC-SAB=
×S△SAB×d,
得d=
=
=
.
(3)解法一:可知
=(0,0,1)是平面ABC一个法向量,故|cos<
,
>|=|
|=
,
二面角S-AB-C的余弦值为
.
(3)解法二:作CH⊥AB于H,作OE∥CH交AB于E,则OE⊥AB,
连接SE,因OE是SE在底面ABC内的射影,而OE⊥AB,故SE⊥AB,∠SEO为二面角S-AB-C的平面角.
△ABC中,易求BA=BC=
,
由△ABC的面积,
×AC×BD=
×AB×CH,CH=
=
,
△AEO与△AHC相似,相似比为AO:AC=3:4,故OE=
CH=
,Rt△SEO中,tan∠SEO=
=
,
故cos∠SEO=
=
,二面角S-AB-C的余弦值为
.
 解:(1)由正视图、俯视图知AC=4;
解:(1)由正视图、俯视图知AC=4;由正视图、侧视图知,点B在平面SAC上的正投影为AC的中点D,则BD=3,BD⊥平面SAC,BD⊥AC;
由俯视图、侧视图知,点S在平面ABC上的正投影为DC的中点O,
则SO=2,SO⊥平面ABC,SO⊥AC.如图.
三棱锥S-ABC的体积VS-ABC=
| 1 |
| 3 |
| 1 |
| 2 |
(2)解法一:
以O为原点,OA为x轴,过O且平行于BD的直线为y轴,OS为z轴,建立如图空间直角坐标系,可求S(0,0,2)A(3,0,0)B(1,3,0),
| SA |
| SB |
设
| m |
|
| m |
| 9 |
| 2 |

可知C(-1,0,0),
| CA |
则d=|
| ||||
|
24
| ||
| 133 |
(2)解法二:可求AB=
| AD2+BD2 |
| 13 |
| AO2+SO2 |
| 13 |
| SO2+OB2 |
| SO2+BD2+DO2 |
| 14 |

△SAB的面积S△SAB=
| 1 |
| 2 |
| 14 |
(
|
| ||
| 2 |
设点C到平面SAB的距离为d,
由三棱锥S-ABC的体积4=VS-ABC=VC-SAB=
| 1 |
| 3 |
得d=
| 12 |
| S△SAB |
| 12 | ||||
|
24
| ||
| 133 |
(3)解法一:可知
| n |
| m |
| n |
| ||||
|
|
9
| ||
| 133 |
二面角S-AB-C的余弦值为
9
| ||
| 133 |
(3)解法二:作CH⊥AB于H,作OE∥CH交AB于E,则OE⊥AB,
连接SE,因OE是SE在底面ABC内的射影,而OE⊥AB,故SE⊥AB,∠SEO为二面角S-AB-C的平面角.
△ABC中,易求BA=BC=
| 13 |
由△ABC的面积,
| 1 |
| 2 |
| 1 |
| 2 |
| AC×BD |
| AB |
12
| ||
| 13 |
△AEO与△AHC相似,相似比为AO:AC=3:4,故OE=
| 3 |
| 4 |
9
| ||
| 13 |
| SO |
| OE |
2
| ||
| 9 |
故cos∠SEO=
| 9 | ||||
|
9
| ||
| 133 |
9
| ||
| 133 |
点评:本题考查的知识点是二面角的平面角及求法,棱锥的体积,点到平面的距离公式,其中(1)的关键是根据已知的三视图判断出几何体的形状及底面棱长,高等关键的几何量,(2)(3)的解法一(向量法)关键是要建立适当的空间坐标系,熟练掌握向量法求距离和夹角的公式.

练习册系列答案
相关题目
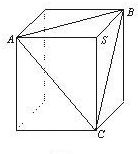 如图,将一个长方体沿相邻三个面的对角线截出一个三棱锥S-ABC,求三棱锥S-ABC的体积与剩下的几何体体积的比.
如图,将一个长方体沿相邻三个面的对角线截出一个三棱锥S-ABC,求三棱锥S-ABC的体积与剩下的几何体体积的比.