题目内容
一个三棱锥S-ABC的三条侧棱SA、SB、SC两两互相垂直,且长度分别为 2、2、4,则S点到平面ABC的距离为( )
分析:先求出△ABC的面积,再利用等体积,即可求得S点到平面ABC的距离.
解答:解:∵三棱锥S-ABC中,共顶点S的三条棱两两互相垂直,且SA=SB=2,SC=4,
∴AB=2
,AC=BC=2
∴AB边上的高为
=3
∴S△ABC=
×2
×3
=6
设S点到平面ABC的距离为h,则由等体积可得
×
×2×2×4=
×6×h
∴h=
即S点到平面ABC的距离为
故选A.
∴AB=2
| 2 |
| 5 |
∴AB边上的高为
| 20-2 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 2 |
| 2 |
设S点到平面ABC的距离为h,则由等体积可得
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
∴h=
| 4 |
| 3 |
即S点到平面ABC的距离为
| 4 |
| 3 |
故选A.
点评:本题考查点到面距离的计算,考查三棱锥体积的计算,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
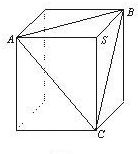 如图,将一个长方体沿相邻三个面的对角线截出一个三棱锥S-ABC,求三棱锥S-ABC的体积与剩下的几何体体积的比.
如图,将一个长方体沿相邻三个面的对角线截出一个三棱锥S-ABC,求三棱锥S-ABC的体积与剩下的几何体体积的比.
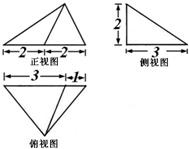 一个三棱锥S-ABC的三视图、直观图如图.
一个三棱锥S-ABC的三视图、直观图如图.